Finding the Inverse of a Function

The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra


Return to Index	Get "Purplemath on CD" for offline use \| Print-friendly page

Finding the Inverse of a Function (page 3 of 7)

Sections: Definition / Inverting a graph, Is the inverse a function?, Finding inverses, Proving inverses

The customary method of finding the inverse is some variant of the method I'm going to use below. Whatever method you use, make sure you do the exact same steps in the exact same order every time, so you remember those steps when you get to the test.

Find the inverse of y = 3x – 2.

Here's how the process works:

Here's my original function:
Now I'll try to solve for "x =":
Now I'll try to solve for "x =":
Once I have "x =", I'll switch x and y; the "y =" is the inverse.

Then the inverse is y = ^{(x
+ 2)} / ₃

If you need to find the domain and range, look at the original function and its graph. The domain of the original function is the set of all allowable x-values; in this case, the function was a simple polynomial, so the domain was "all real numbers". The range of the original function is all the y-values you'll pass on the graph; in this case, the straight line goes on for ever in either direction, so the range is also "all real numbers". To find the domain and range of the inverse, just swap the domain and range from the original function.

Find the inverse function of y = x² + 1, if it exists.

There will be times when they give you functions that don't have inverses.

From the graph, it's easy to see that this function can't possibly have an inverse, since it violates the Horizontal Line Test:

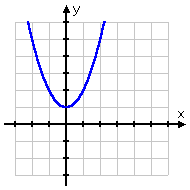
function without an inverse function

It is usually considered acceptable to draw the above graph, draw a horizontal line across it that crosses the graph twice, and then say something like "The inverse of this function is not itself a function, because of the Horizontal Line Test". But some teachers want to see the algebra anyway. Be sure to check with your teacher and verify what will be an acceptable answer -- and do this before the test! Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved

What will this look like when I try to find the inverse algebraically? The Vertical Line Test says that I can't have two y's that share an x-value. That is, each x has to have a UNIQUE corresponding y value. But look at what happens when I try to solve for "x =":

My original function:
Solving for "x =":
Solving for "x =":

Well, I solved for "x =", but I didn't get a UNIQUE "x =". Instead, I've shown that any given x-value will actually correspond to two different y-values, one from the "plus" on the square root and the other from the "minus".

The inverse is not a function.

Any time you come up with a "±" sign, you can be pretty sure that the inverse isn't a function.

Find the inverse function of y = x² + 1, x < 0.

The only difference between this function and the previous one is that the domain has been restricted to only the negative half of the x-axis. This restriction makes the graph look like this:

y = x^2 + 1, x <= 0

This function will have an inverse that is also a function. Just about any time they give you a problem where they've taken the trouble to restrict the domain, you should take care with the algebra and draw a nice picture, because the inverse probably is a function, but it will probably take some extra effort to show this. In this case, since the domain is x < 0 and the range (from the graph) is 1 < y, then the inverse will have a domain of 1 < x and a range of y < 0. Here's how the algebra looks:

The original function:
Solve for "x =":


By figuring out the domain and range of the inverse, I know that I should choose the negative sign for the square root:
Now I'll switch the x and y; the new "y =" is the inverse: