Definition of "Inverse" & Inverting from a Graph
Is Inverse a Function?Finding InversesRestricted DomainsWorked ExamplesQuarter-CirclesProving Inverses
Purplemath
Your textbook's coverage of inverse functions probably came in two parts. The first part had lots of curly-braces and lists of points; the second part has lots of "y=" or "f(x)=" functions for which you have to find the inverses, if possible.
The first part (with the sets of points) will show up in your homework and maybe on a test; the second part (with the equations) will definitely show up on your test, and you might even use it in later classes.
Content Continues Below
What is a relation in math?
In mathematics, a "relation" is a pairing of values. The pairing may be represented as a list of ordered pairs, or it may be represented by a formula. For instance, the following list of points is a relation:
{ (0, −1), (−3, 2), (47, −1) }
The formula for a circle of radius r centered at the origin is x2 + y2 = r2, and is also a relation, because it relates to each other the values of x and y.
What is the inverse of a relation?
The inverse of a relation has all the same points as the original relation, except that the x's and y's have been reversed. To find ("create"?) the inverse for a given list-of-points relation, that's all you do: you reverse the x's and y's.
For instance, supposing your relation is made up of these points:
{ (1, 0), (−3, 5), (0, 4) }
Then the inverse of the relation is given by this set of points:
{ (0, 1), (5, −3), (4, 0) }
Advertisement
(Note that the order of the points doesn't matter; you can rearrange the points so the x's are "in order", or not. It's your choice.)
Affiliate
Your textbook started off with relations, but quickly turned to functions. Keep in mind the difference between these two.
What is the difference between a function and a relation?
A relation is just a pairing of information; a function is a well-behaved relation. In particular, a function passes the Vertical Line Test, which confirms that no one x-value ever goes to more than one y-value; no vertical line will cross a function's graph more than once.
With a relation, on the other hand, all bets are off.
When they've started you off with a function, which is a well-behaved relation, the question then becomes, "Is the inverse also a function? Is the inverse also well-behaved?"
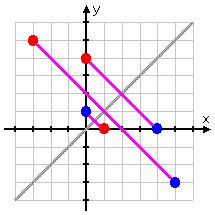
The relation we started with was this listing of points:
{ (1, 0), (−3, 5), (0, 4) }
We can plot these points; the resulting graph looks like this:
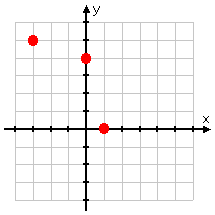
Because there are no two distinct points that share the same x-value, you can know that this is a function (and you can check quickly by using the Vertical Line Test). The inverse graph is the blue dots below:
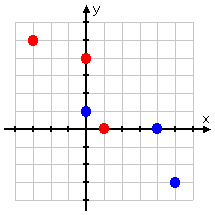
The blue dots (being the set of points that represent the inverse of the original set) don't have any two points sharing an x-value. This means that the inverse is also a function.
Content Continues Below
You can use the Mathway widget below to practice finding the inverse of relations consisting of sets of points. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Relation Inverse" to compare your answer to Mathway's. (Or skip the widget and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
How do you find the inverse from a graph?
Your textbook probably went on at length about how the inverse is "a reflection in the line y = x". What it was trying to say was that you could take your function, draw the line y = x (which is the diagonal line from the bottom-left to the top-right), put a two-sided mirror on this line, and you could "see" the inverse reflected in the mirror. Practically speaking, this "reflection" property can help you draw the inverse:
Draw the points and the reflection line:
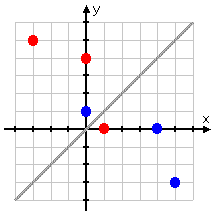
Reflect the points across the line:
You can see on this last picture that there is a definite graphical relationship between the points of the function and the points of the inverse. You can use this relationship if you're given a random graph and are told to graph the inverse.
Suppose you are asked to find the inverse of the function given this graph:
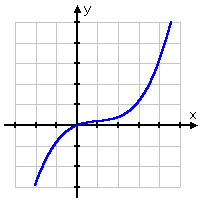
Note that I have NOT told you what that function is.
To get started finding the inverse, draw the reflection line:
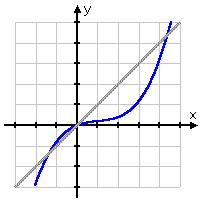
(It would be a good idea to use a ruler for this; you'll want to be neat.)
Now eyeball the graph, and draw the diagonals from known points on the graph to their "reflections" on the other side of the line:
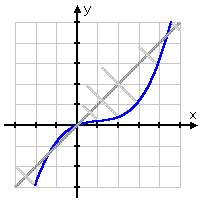
Note that the points actually ON the line y = x don't move; that is, where the function crosses the diagonal, the inverse will cross the diagonal, too.
Now draw in some plot-points:
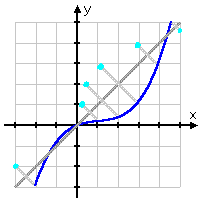
...and connect the dots:
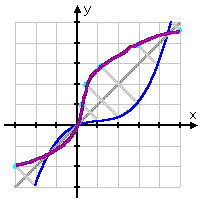
Without ever knowing what the rule or formula for the original function (the blue line), you can draw the inverse (the purple line).
URL: https://www.purplemath.com/modules/invrsfcn.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()