Venn Diagrams: Exercises
Purplemath
Venn diagram word problems generally give you two or three classifications and a bunch of numbers. You then have to use the given information to populate the diagram and figure out the remaining information. For instance:
-
Out of forty students, 14 are taking English Composition and 29 are taking Chemistry.
- If five students are in both classes, how many students are in neither class?
- How many are in either class?
- What is the probability that a randomly-chosen student from this group is taking only the Chemistry class?
Content Continues Below
There are two classifications in this universe: English students and Chemistry students.
First I'll draw my universe for the forty students, with two overlapping circles labelled with the total in each:
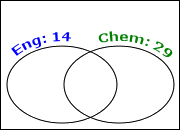
(Well, okay; they're ovals, but they're always called "circles".)
Five students are taking both classes, so I'll put "5" in the overlap:
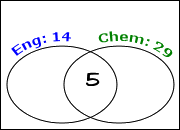
I've now accounted for five of the 14 English students, leaving nine students taking English but not Chemistry, so I'll put "9" in the "English only" part of the "English" circle:
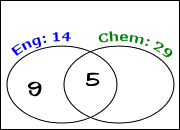
I've also accounted for five of the 29 Chemistry students, leaving 24 students taking Chemistry but not English, so I'll put "24" in the "Chemistry only" part of the "Chemistry" circle:
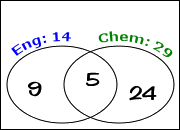
This tells me that a total of 9 + 5 + 24 = 38 students are in either English or Chemistry (or both). This gives me the answer to part (b) of this exercise. This also leaves two students unaccounted for, so they must be the ones taking neither class, which is the answer to part (a) of this exercise. I'll put "2" inside the box, but outside the two circles:
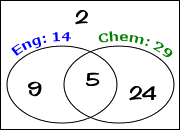
The last part of this exercise asks me for the probability that a agiven student is taking Chemistry but not English. Out of the forty students, 24 are taking Chemistry but not English, which gives me a probability of:
- Two students are taking neither class.
- There are 38 students in at least one of the classes.
- There is a 60% probability that a randomly-chosen student in this group is taking Chemistry but not English.
Content Continues Below
-
Years ago, I discovered that my (now departed) cat had a taste for the adorable little geckoes that lived in the bushes and vines in my yard, back when I lived in Arizona. In one month, suppose he deposited the following on my carpet:
- six gray geckoes,
- twelve geckoes that had dropped their tails in an effort to escape capture, and
- fifteen geckoes that he'd chewed on a little
In addition:
- only one of the geckoes was gray, chewed-on, and tailless;
- two were gray and tailless but not chewed-on;
- two were gray and chewed-on but not tailless.
If there were a total of 24 geckoes left on my carpet that month, and all of the geckoes were at least one of "gray", "tailless", and "chewed-on", how many were tailless and chewed-on, but not gray?
If I work through this step-by-step, using what I've been given, I can figure out what I need in order to answer the question. This is a problem that takes some time and a few steps to solve.
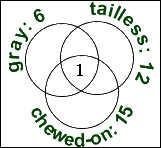
They've given me that each of the geckoes had at least one of the characteristics, so each is a member of at least one of the circles. This means that there will be nothing outside of the circles; the circles will account for everything in this particular universe.
There was one gecko that was gray, tailless, and chewed on, so I'll draw my Venn diagram with three overlapping circles, and I'll put "1" in the center overlap:
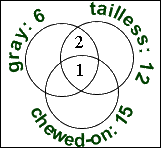
Two of the geckoes were gray and tailless but not chewed-on, so "2" goes in the rest of the overlap between "gray" and "tailless".
Two of them were gray and chewed-on but not tailless, so "2" goes in the rest of the overlap between "gray" and "chewed-on".
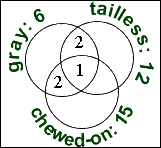
Since a total of six were gray, and since 2 + 1 + 2 = 5 of these geckoes have already been accounted for, this tells me that there was only one left that was only gray.
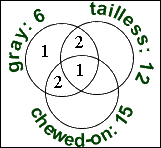
This leaves me needing to know how many were tailless and chewed-on but not gray, which is what the problem asks for. But, because I don't know how many were only chewed on or only tailless, I cannot yet figure out the answer value for the remaining overlap section.
I need to work with a value that I don't yet know, so I need a variable. I'll let "x" stand for this unknown number of tailless, chewed-on geckoes.
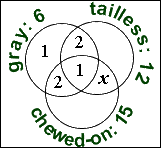
I do know the total number of chewed geckoes (15) and the total number of tailless geckoes (12). After subtracting, this gives me expressions for the remaining portions of the diagram:
only chewed on:
15 − 2 − 1 − x = 12 − x
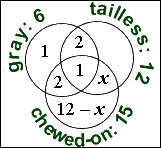
only tailless:
12 − 2 − 1 − x = 9 − x
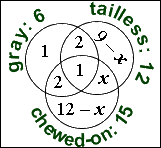
There were a total of 24 geckoes for the month, so adding up all the sections of the diagram's circles gives me: (everything from the "gray" circle) plus (the unknown from the remaining overlap) plus (the only-chewed-on) plus (the only-tailless), or:
(1 + 2 + 1 + 2) + (x)
+ (12 − x) + (9 − x)
= 27 − x = 24
Solving, I get x = 3. So:
Three geckoes were tailless and chewed on but not gray.
(No geckoes or cats were injured during the production of the above word problem.)
For more word-problem examples to work on, complete with worked solutions, try this page provided by Joe Kahlig of Texas A&M University. There is also a software package (DOS-based) available through the Math Archives which can give you lots of practice with the set-theory aspect of Venn diagrams. The program is not hard to use, but you should definitely read the instructions before using.
URL: https://www.purplemath.com/modules/venndiag4.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



