Multiplying Rational Expressions
Purplemath
With regular fractions, multiplying and dividing is fairly simple, and is much easier than adding and subtracting. The situation is much the same with rational expressions (that is, with polynomial fractions).
The only major problem I have seen students having with multiplying and dividing rationals is with illegitimate cancelling, where they try to cancel terms instead of factors, so I'll be making a big deal about this issue as we go along.
Content Continues Below
Remember how you multiply regular fractions: You multiply across the top and bottom. For instance, the following multiplied fractions:
And you need to simplify, whenever possible:
Affiliate
While the process and order of steps in the above simplification are perfectly valid, it is generally simpler to cancel first and then do the multiplication. By cancelling first, you'll then be dealing with smaller numbers.
In the above example, the 3 in the numerator of the first fraction duplicates a factor of 3 in the denominator of the second fraction, and the 5 in the denominator of the first fraction duplicates a factor of 5 in the numerator of the second fraction. Since anything divided by itself is just 1, we can "cancel out" these common factors (that is, we can ignore these forms of the number 1) to find a simpler form of the fraction:
This process (cancelling, then multiplying) works with rational expressions, too.
How do you multiply rational expressions?
- Factor all of the polynomials.
- Cancel off any common factors.
- Multiply things out in the resulting numerator.
The third step above may be omitted, if your instructor doesn't care. And, on occasion, an instructor will want the denominator multiplied out, in addition to the numerator. Make sure you are clear on what your instructor wants here.
What is an example of multiplying rational expressions?
- Simplify the following rational-expression multiplication:
The first thing I notice is the variable in the denominator of the second fraction. The x cannot be allowed to be equal to zero, because this would cause division by zero, which is forbidden.
I will start my simplification by cancelling off duplicate factors. Then I'll multiply together whatever is left. My working looks like this:
(If you're not sure how the variable parts were simplified above, you may want to review how to simplify expressions with exponents.)
There's nothing else that cancels; there is nothing else to multiply together. I've done all I can do with respect to simplification. However, my answer above is not technically equal to the original expression. Why not? Because my end expression can have x = 0, which wasn't true of the expression they gave me at the beginning. So my (completely equal) answer is:
Content Continues Below
I added the "for x not equal to 0" restriction to my simplified rational expression because the original expression was not "defined" at x = 0; that is to say, it would have had no mathematical meaning; it would not have made mathematical sense. This is because allowing the variable to be zero would have caused division by zero in the second of the two original fractions. And we can never divide by zero.
Why are restrictions added to simplified rational expressions?
For two expressions, the original one and its simplified form, to be "equal" in technical terms, their domains must be the same; they have to be defined for the same x-values. Since the simplified fraction form in my answer above, being 3x/2, has no division-by-zero problem at x = 0 (because cancelling got rid of the variable in the denominator), it is not, strictly-speaking, "equal" to the original expression. To make the simplified form truly equal to the original form, I have to explicitly state this "x cannot be zero" exclusion.
Be advised: Your particular textbook or instructor might not make this distinction. If you're not sure if your teacher cares about this technicality, please make sure to ask before the next test.
- Multiply and simplify the following:
Many students find it helpful to convert the "15" into a fraction. This can make the factors a little more obvious, so one can see more clearly what can cancel with what. So I'll start with oonverting the 15 into fractional form, and then I'll start the simplification process.
My work looks like this:
At this stage, can I cancel the 2 from the denominator into the 20 in one of the terms in the numerator? No!
"But why not?", I hear you ask.
Why can't we cancel terms with terms?
Because, when we have a fractional expression, there are understood parentheses around any sums of terms. And we can't go inside parentheses and cancel only a portion of what is contained within those parentheses. To be explicit by adding the parentheses to the vertical fraction under discussion, we get something that looks like this:
Imagine that the x in the above were equal to 1. Then the fraction would be:
(20 + 5)/2
Advertisement
Now imagine that I took the 2 from the denominator, smashed my way inside the parentheses around the numerator, and mugged the 20 in the numerator. I'd get something like (10 + 5)/(1), which equals 15. But (25)/2 = 12.5, not 15!
Attempting to cancel just a portion of a parenthetical is mathematically illegitimate. When reducing fractions and rational expressions, we can only cancel entire "common factors", not mere bits and pieces of larger expressions.
By the way, while we often don't think about this unstated grouping — especially when the fraction is stacked vertically the way it always is when nice mathematical formatting is available — that grouping is always there, regardless of whether or not the parentheses are there to make the grouping explicit. This implicit grouping is more obvious when the fraction is written out sideways, the way one might do in an email or a forum posting:
(20x + 25)/(2)
Without the grouping symbols, the above would have been written as:
20x + 25/2
The above puts the fraction as containing only 25 in the numerator; the 20x is a separate term. So, without the grouping symbols in our horizontal (that is, our sideways) formatting, we would have actually been saying this:
But this is totally not what we meant!
Affiliate
When simplifying rational expressions, we can only cancel off factors (the entire contents of a set of parentheses); we can NOT cancel terms; that is to say, we cannot reach inside a set of parentheses, implicit or otherwise, and work with only part of what is inside those parentheses. Barging inside those parentheses, willy-nilly hacking x's and y's and arms and legs off the poor polynomials, doesn't "simplify" anything; it just leaves the sad little polynomial lying there on the floor, quivering and bleeding and oozing and whimpering...
Okay, maybe not; but I hope you understand my point: Never reach inside the parentheses and hack off part of the contents. Either you cancel off the entire contents of a parenthetical or factor with a matching parenthetical or factor from the other side of the fraction line, or you do NOT cancel anything at all.
In my simplification above, the only thing that I could factor out of the numerator (being the 20x + 25) was a 5, and that factor didn't cancel with the 2 underneath, so, for this rational, there is no further reduction to be done. Then my final answer is:
(Your instructor may care whether or not the factors in the final expression are muiltiplied out, left factored, only multiplied out in the numerator, or some other variation. Just in case it matters, ask now if your instructor has a preference.)
- Multiply and simplify the following:
I'll turn to completing this exercise shortly. But first, let's have us a little chat.
Some students, when faced with this problem, will do something like this:
NEVER DO THIS!
😱 NOT EVER!! 🤮
Can we really "cancel" like this? (Think "bleeding"...) Is this even vaguely legitimate? (Oozing...) Were I to do this, would I have done anything at all correctly? (Flopping, whimpering...) No, no, and no!
You can NOT cancel terms.
you can ONLY cancel factors.
Phew! Okay; now that I've got that out of my system, let's get back to the exercise.
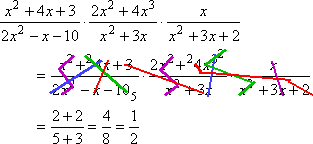
Since I can only cancel factors, my first step in this simplification has to be to factor all the numerators and denominators. Once I've factored everything, I can cancel off any factor that is mirrored on the two sides of the fraction line.
They have given me this expression to multiply and simplify:
First, I'll factor everything:
Can I now cancel off, say, the 2x inside the first factor in the bottom of the first fraction with the 2x2 from the first factor in the top of the second fraction? (Tears are welling up in the polynomial's eyes...) Can I cancel off the x inside the 1 +2x factor on top of the second fraction with the x inside x + 2 from the bottom of the first fraction? (Now the polynomial is starting to cry...) No! The 2x, the 2x2, and the x's are only parts of their respective factors; they are not stand-alone factors, so they can't cancel off with anything.
No; the only things I can cancel are entire factors from opposite sides of the fraction lines, where those factors are exactly and entirely the same. So my cancellation looks like this:
(In the above, I multiplied everything out at the end, so you can see what it would look like. In general, though, it's often fine to quit once the duplicate factors are cancelled off. In my hand-in answer, I'll use the multiplied-out numerator, but I'll revert the denominator back to factored form. When adding rational expressions, this "terms across the top, with factors across the bottom" thing can be a very important consideration. For now, just keep in mind that it's a formatting option.)
So my answer — taking note of the trouble-spots (that is to say, taking note of the values which would create division-by-zero problems) that I removed when I cancelled the common factors — is the following:
The restrictions on my answer, being the "x not equal to 0, −1 or −3", came from the denominators' factors that I had cancelled off; namely, from the x, x + 1, and x + 3 factors, respectively. Your book may not require this information as part of your answer.
Note: For reasons which will become clear when you are adding rational expressions, it is customary to leave the denominator factored, as shown above. At this stage, your book may be okay with the numerator being left factored, or it may prefer that the numerator be multiplied out.
You should be able to recognize, in any case, that "(2x − 5)(x + 2)2" is the same thing as "2x3 + 3x2 − 12x − 20", and get in the habit of converting the form of your answer to match that of your textbook or instructor, if either of these seems to expect your answers to be written in a particular way.
URL: https://www.purplemath.com/modules/rtnlmult.htm
You can use the Mathway widget below to practice multiplying rational expressions (or skip the widget, and continue to the next page). Try the entered exercise, or type in your own exercise. Then click the button and select "Simplify" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




