Reducing Fractions
Purplemath
What is a fraction?
A fraction is a ratio of two whole numbers, such as ¾. The number on top is called the numerator; the number underneath is called the denominator. The word numerator is derived from a Latin word meaning "counter"; the word denominator is derived from a Latin word meaning "name".
Content Continues Below
In essence, the denominator names how many pieces something has been split into; the numerator counts how many of those pieces you're working with.
What does it mean to "reduce" a fraction?
Reducing a fraction to its lowest terms is the process of eliminating duplicate factors shared by the numerator (that is, the top number) and the denominator (that is, the bottom number), resulting in a fraction that is equal to the original, but which has no extra information.
For instance, the fraction is the same number (that is, it has the same value) as and , but only the fraction is fully reduced.
In what follows, it will sometimes be useful to remember that fractions can indicate division. For instance, can mean "one divided by three" as well as ""one part out of three parts". In fact, let's cut to the chase; memorize this sentence:
Fractions are division.
You learned long ago that any number, divided by itself, is just 1. We use this fact when we reduce fractions. If we can convert part of a given fraction into being a multiplied form of 1, then we can ignore this part, because multiplying by 1 doesn't change anything.
For instance, here's how we can find and use a form of 1 to reduce the fraction 4/8 to lowest terms (that is, how we can reduce it to simplest form):
To be very clear, the point of finding the common factor (in this case, the 4's) is to allow you to convert part of the fraction to 1. Since equals 1, then what I did above was the following:
![4/8 = (1/2)*[(4/4), which is 1] = (1/2)*(1) = 1/2](fraction/frac01A.png)
Affiliate
Advertisement
Important aside: Note how I switched from one fraction containing two products (in the numerator and denominator):
...to one product of two fractions:
This switch is okay as long as you're multiplying:
...but it is very much NOT okay if we're adding. For instance:
The left-hand side above, being a fraction containing addition, is equal to , while the right-hand side above, being an addition containing fractions, is equal to , so the two expressions are not at all the same value. Just remember: For fractions, multiplying is way easier than adding. Now, to get back to business...
Content Continues Below
In addition to the canceling method I used above (with the pink 1's), you may also have seen either of the following "shorthands" for cancellation:
Any of these formats is fine. The two shorthand methods are probably simplest for your handwritten homework.
Affiliate
Can my calculator reduce fractions for me?
If you have a regular calculator (that is, if you have a scientific or business calculator) that can handle fractions, then you can enter the fraction and then hit the "equals" button to get the reduced fraction. If you have a graphing calculator with a fraction command, then you can enter the fraction as a division (because means "four divided by eight"), and then convert to fraction form. Check your calculator's owners manual for specifics.
If your calculator can't handle fractions, or if the denominator is too large for the calculator to handle, then you'll need to do the reduction by hand.
Either way, you'll need the concept and methodology of fraction-reduction in later algebra courses, when you're working with polynomial fractions.
How do you reduce a fraction?
To reduce a fraction, follow these steps:
- Factor the numerator and denominator.
- Note any factors which are common to the numerator and denominator.
- Cancel off pairs of common factors.
- Multiply together whatever remains after cancellation.
Remember that if "everything" cancels out of, say, the numerator, then there still remains a factor of 1. Everything is always multiplied by 1, but we don't usually pay any attention to this. However, if all of the non-trivial factors (that is, if all the factors that aren't 1) get cancelled by matching factors on the other side of the fraction line, then you've still got that 1; the fraction does not become headless.
By the way, the proper name for the fraction line is "vinculum" (VINK-yoo-lumm). No, you don't really need to know this.
What is an example of reducing a fraction to lowest terms?
- Reduce to simplest form.
I'll grab my calculator and some scrap paper, and factor the numerator (top number) and denominator (bottom number). A quick shorthand for getting the prime factorization of each of these numbers is demonstrated below, in the stacked division (by prime numbers) of 2940:
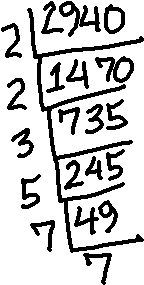
To find the factorization, I just read off the prime factors from around the outside of the upside-down division. From the above, I can see that 2940 factors as 2×2×3×5×7×7.
Next, I'll factor the denominator, being the number 3150:
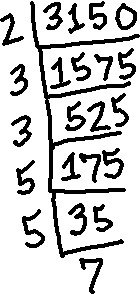
So 3150 factors as 2×3×3×5×5×7.
Now I can reduce the fraction by canceling off the common factors:
So, after cancelling all the factors that were duplicated in (that is, after crossing out all the factors that were common to) the numerator and denominator, my reduced-form answer is:
You can use the Mathway widget below to practice reducing fractions. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's. Or skip the widget, and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/fraction.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()