Factoring Numbers
Purplemath
What are a number's "factors"?
"Factors" are the whole numbers you multiply to get another whole number. For instance, factors of 15 are 3 and 5, because 3 × 5 = 15. Some numbers have more than one factorization (more than one way of being factored). For instance, 12 can be factored as 1 ×12, 2 × 6, and also as 3 × 4.
Content Continues Below
What is a "prime" number? What is a "composite" number?
A number that can only be factored as 1 times itself is called "prime". The first few primes are 2, 3, 5, 7, 11, and 13. Numbers that have "non-trivial" factors (that is, numbers which have factors other than just 1 and itself) are "composite" numbers, because they are composed of non-trivial factors.
Is 1 a prime or composite number?
The number 1 is not regarded as a prime, and is usually not included in factorizations, because 1 goes into everything. But 1 has only itself (twice!) as factors, so it isn't a composite number, either. The number 1 is a bit boring in this context — being neither prime nor composite — so it mostly gets ignored.
What is prime factorization?
The prime factorization of a number is the product of all the prime-number factors of a given number, including the number of times each of the primes is a factor. The prime factorization does not include 1, but does include every copy of every prime factor.
When factoring a number, you most often want to find the prime factorization of that number. For instance, the prime factorization of 8 is 2×2×2, not just 2. Yes, 2 is the only prime factor of 8, but you need three copies of it to multiply back to 8, so the prime factorization includes all three copies.
prime factors of 8: 2
prime factorization of 8: 2 × 2 × 2 = 23
Affiliate
On the other hand, the prime factorization includes ONLY the prime factors, not any products of those factors. For instance, even though 2 × 2 = 4, and even though 4 is a divisor of 8, 4 is NOT in the PRIME factorization of 8. That is because 8 does NOT equal 2 × 2 × 2 × 4.
This accidental over-duplication of factors is another reason why the prime factorization is often best: it avoids counting any factor too many times.
Suppose that you need to find the prime factorization of 24. Sometimes a student will just list all the divisors of 24: 1, 2, 3, 4, 6, 8, 12, and 24. Then the student will do something like make the product of all these divisors:
1 × 2 × 3 × 4 × 6 × 8 × 12 × 24
But this equals 331776, not 24. So it's best to stick to the prime factorization, even if the problem doesn't require it, in order to avoid either omitting a factor or else over-duplicating one.
Advertisement
In the case of 24, you can find the prime factorization by taking 24 and dividing it by the smallest prime number that goes into 24: 24 ÷ 2 = 12. (Actually, the "smallest" part is not as important as the "prime" part; the "smallest" part is mostly to make your work easier, because dividing by smaller numbers is simpler.)
Now divide out the smallest number that goes into 12: 12 ÷ 2 = 6.
Now divide out the smallest number that goes into 6: 6 ÷ 2 = 3. And, because 3 is prime, you're now done factoring, and the prime factorization is 2 × 2 × 2 × 3.
Advertisement
What is an easy way to do prime factorization?
An easy way of keeping track of the factorization is to do continued division; it looks like this:
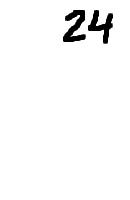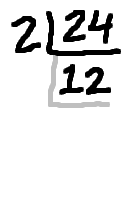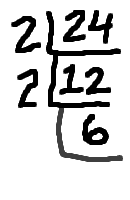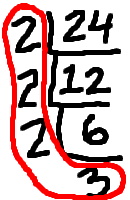
(The above graphic is animated on the "live" page.)
The nice thing about this continued division is that, when you're done, the prime factorization is the product of all the numbers around the outside. The factors are circled in red above. By the way, this continued division is something that should probably be done on scratch-paper, and not handed in as part of your homework.
(If you prefer doing your continued division right-side up, rather than upside-down as shown above, that's perfectly fine.)
What is an example of doing prime factorization?
- Find the prime factorization of 1050.
I'll do the continued division, starting by dividing by 2:

(The above graphic is animated on the "live" page.)
Reading around the outside, I find that my answer is:
1050 = 2 × 3 × 5 × 5 × 7
Some texts prefer that answers such as this be written using exponential notation, in which case the final answer would be written as 2×3×52×7.
As mentioned above, you can do the continued division right-side up, too, if you prefer. The process works the same either way, but the division is reversed in orientation. The above example would be worked out like this:
- Find the prime factorization of 1092.
I'll do the repeated division:
Reading around the outside, I can see that the prime factorization is:
1092 = 2 × 2 × 3 × 7 × 13
This answer can also be written in exponential notation as 22 × 3 × 7 × 13.
Content Continues Below
What is the difference between finding the prime factors of a number, and finding that number's prime factorization?
Finding the prime factors of a number starts with the division of the number by various primes, until you've found all of the primes that divide into that number; the result is a list of prime numbers that are factors. On the other hand, finding the prime factorization of the number starts with the same division process, but ends with a product of the prime factors, showing every copy of each prime that is needed to produce the original number. For the number 900, the difference looks like this:
prime factors: 2, 3, 5
prime factorization: 2 × 2 × 3 × 3 × 5 × 5
What are some divisibility rules that can help with prime factorizations?
There are many divisibility rules that can help you with prime factorizations, but the simplest to use are these:
- If the number is even, then it's divisible by 2.
- If the number's digits sum to a number that's divisible by 3, then the number itself is divisible by 3.
- If the number ends with a 0 or a 5, then it's divisible by 5.
Of course, if the number is divisible twice by 2, then it's divisible by 4; if it's divisible by 2 and by 3, then it's divisible by 6; and if it's divisible twice by 3 (or if the sum of the digits is divisible by 9), then it's divisible by 9. But since you're finding the prime factorization, you don't really care about these non-prime divisibility rules.
There are rules for divisibility by 7 (such as here and here), but you'll probably find it to be easier to just do the division on your calculator and see if the result of the division comes out to be a whole number. (If you're interested, there is a circle-graph that you can use, or else a double-the-ones-digit method that you can apply as many times as needed.)
Affiliate
If you've run out of the smaller primes but you're not sure that done factoring, then keep trying bigger and bigger primes (11, 13, 17, 19, 23, etc) until you find something that works — or until you reach a prime where your answer is smaller than the prime you're trying to divide by.
Why do you stop trying prime divisors once once you reach a prime that gives a too-small answer?
If your prime doesn't divide in to whatever is the result you're trying to factor, then the only potential prime divisors of that result are still-bigger prime numbers. Since the result of dividing by your prime is smaller than the number you're trying to divide into, then all bigger primes will be even less helpful. So the number left must itself be prime, and you're done.
Why do we need to learn factorization?
When finding the least common multiple (or lowest common denominator) or greatest common factor, it can be extremely helpful to find the prime factorizations. This is especially true when you're working with larger numbers, or with algebraic expressions like polynomials.
You can use the Mathway widget below to practice finding the prime factorization. Try the entered exercise, or type in your own exercise. Then click the button and choose "Find the Prime Factorization" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Clicking on "Tap to view steps" on the widget's answer screen will take you to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/factnumb.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()