The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Number Bases:
  Introduction / Binary Numbers (page 1 of 3)

Sections: Introduction & binary numbers, Base 4 & base 7, Octal & hexadecimal

Converting between different number bases is actually fairly simple, but the thinking behind it can seem a bit confusing at first. And while the topic of different bases may seem somewhat pointless to you, the rise of computers and computer graphics has increased the need for knowledge of how to work with different (non-decimal) base systems, particularly binary systems (ones and zeroes) and hexadecimal systems (the numbers zero through nine, followed by the letters A through F).

In our customary base-ten system, we have digits for the numbers zero through nine. We do not have a single-digit numeral for "ten". Yes, we write "10", but this stands for "1 ten and 0 ones". This is two digits; we have no single solitary digit that stands for "ten".

Instead, when we need to count to one more than nine, we zero out the ones column and add one to the tens column. When we get too big in the tens column -- when we need one more than nine tens and nine ones ("99"), we zero out the tens and ones columns, and add one to the ten-times-ten, or hundreds, column. The next column is the ten-times-ten-times-ten, or thousands, column. And so forth, with each bigger column being ten times larger than the one before. We place digits in each column, telling us how many copies of that power of ten we need.

The only reason base-ten math seems "natural" and the other bases don't is that you've been doing base-ten since you were a child. And (nearly) every civilization has used base-ten math probably for the simple reason that we have ten fingers. If instead we lived in a cartoon world, where we would have only four fingers on each hand (count them next time you're watching TV or reading the comics), then the "natural" base system would likely have been base-eight, or "octal".

Binary

Let's look at base-two, or binary, numbers. How would you write, for instance, 12₁₀ ("twelve, base ten") as a binary number? You would have to convert to base-two columns, the analogue of base-ten columns. In base ten, you have columns or "places" for 10⁰ = 1, 10¹ = 10, 10² = 100, 10³ = 1000, and so forth. Similarly in base two, you have columns or "places" for 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, and so forth.

The first column in base-two math is the units column. But only "0" or "1" can go in the units column. When you get to "two", you find that there is no single solitary digit that stands for "two" in base-two math. Instead, you put a "1" in the twos column and a "0" in the units column, indicating "1 two and 0 ones". The base-ten "two" (2₁₀) is written in binary as 10₂.

A "three" in base two is actually "1 two and 1 one", so it is written as 11₂. "Four" is actually two-times-two, so we zero out the twos column and the units column, and put a "1" in the fours column; 4₁₀ is written in binary form as 100₂. Here is a listing of the first few numbers:

Converting between binary and decimal numbers is fairly simple, as long as you remember that each digit in the binary number represents a power of two.

• Convert 101100101₂ to the corresponding base-ten number.

I will list the digits in order, and count them off from the RIGHT, starting with zero:

digits:	1  0   1  1  0  0  1  0  1
numbering:	8  7   6  5  4  3  2  1  0

The first row above (labelled "digits") contains the digits from the binary number; the second row (labelled " numbering") contains the power of 2 (the base) corresponding to each digits. I will use this listing to convert each digit to the power of two that it represents:

1×2⁸ + 0×2⁷ + 1×2⁶ + 1×2⁵ + 0×2⁴ + 0×2³ + 1×2² + 0×2¹ + 1×2⁰

    = 1×256 + 0×128 + 1×64 + 1×32 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1

    = 256 + 64 + 32 + 4 + 1

    = 357   Copyright © Elizabeth Stapel 2001-2011 All Rights Reserved

Then 101100101₂ converts to 357₁₀.

Now YOU try it!

Converting decimal numbers to binaries is nearly as simple: just divide by 2.

• Convert 357₁₀ to the corresponding binary number.

To do this conversion, I need to divide repeatedly by 2, keeping track of the remainders as I go. Watch below:

As you can see, after dividing repeatedly by 2, I ended up with these remainders:

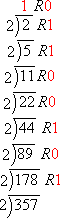
These remainders tell me what the binary number is. I read the numbers from around the outside of the division, starting on top and wrapping my way around and down the right-hand side. As you can see:

357₁₀ converts to 101100101₂.

Now YOU try it!

This method of conversion will work for converting to any non-decimal base. Just don't forget to include that first digit on the top, before the list of remainders. If you're interested, an explanation of why this method works is available here.

You can convert from base-ten (decimal) to any other base. When you study this topic in class, you will probably be expected to convert numbers to various other bases, so let's looks at a few more examples.

Top  |  1 | 2 | 3  |  Return to Index  Next >>

  Copyright © 2001-2012  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?