Sequence Patterns & The Method of Common Differences
Purplemath
What is a sequence?
A sequence is a comma-separated list; in mathematics, a sequence is a listing of numerical values. The sequence may have a rule for its comma-separated terms, or its values may be completely random.
Lists of random values are not very interesting mathematically, so you will almost always be working with sequences that have controlling rules. The terms in these lists will almost always be whole numbers.
When faced with a sequence for which you need to find missing values or the next few values, you need first to look at it and see if you can get a feel for what is going on. Many sequences, at least when you're starting out, have fairly simple rules. You should look for even numbers, odd numbers, squares, cubes, and the like. For instance:
- Find the next number in the following sequence: 1, 4, 9, 16, 25,....
I notice the following:
n = 1 ⇒ 12 = 1
n = 2 ⇒ 22 = 4
n = 3 ⇒ 32 = 9
n = 4 ⇒ 42 = 16
n = 5 ⇒ 52 = 25
Where did the n come from? It is the index of the sequence; it is the counter for the terms of the sequence. When n = 1, I'm looking at the first term of the sequence; when n = 14, I'm looking at the fourteenth term of the sequence. And so forth.
From my listing above it looks as though the pattern for the terms of this sequence is squaring. That is, for the first term (the 1-st term), it looks like they squared 1; for the second term (the 2-nd term), they squared 2; for the third term (the 3-rd term), they squared 3; and so on. For the n-th term ("the enn-eth term"), they will probably want me to square n. In particular, for the sixth term, they will probably want me to square 6.
So my answer for the next number in the sequence is:
62 = 36
Why is the answer only "probably" the square of six? Because "the right answer" is nothing more than whatever answer the authors had in mind when they designed the exercise; you might see a completely different pattern that they hadn't intended. But as long as your answer is something that you can mathematically (or at least logically) justify, your answer should be acceptable, even if it isn't the expected answer.
- Find the next number in the following sequence: 1, 4, 27, 256,....
This pattern looks similar to the previous sequence, in that I'm seeing powers. But, while 12 = 1 and 22 = 4, the next term is *not* a square (of a whole number). But the next term does represent a power: 33 = 27. So..., hmm...
The number 1, raised to any power, will still be 1. So maybe the pattern is the number (equal to the index) raised to the power of the index. Lemme check:
n = 1 ⇒ 11 = 1
n = 2 ⇒ 22 = 4
n = 3 ⇒ 33 = 27
n = 4 ⇒ 44 = 256
So the pattern seems to be that the n-th term is of the form nn. Then the next term, being the fifth term (so n = 5) is:
55 = 3125
- Find the next number in the following sequence: 2, 5, 10, 17, 26,....
I have to be more clever to figure out the pattern on this sequence. Each term is 1 more than a square. That is, the pattern is given by:
n |
n2 |
n2 + 1 |
|---|---|---|
1 |
12 = 1 |
1 + 1 = 2 |
2 |
22 = 4 |
4 + 1 = 5 |
3 |
32 = 9 |
9 + 1 = 10 |
4 |
42 = 16 |
16 + 1 = 17 |
5 |
52 = 25 |
25 + 1 = 26 |
So it looks like the n-th term is given by n2 + 1. Then the sixth term is:
62 + 1 = 36 + 1 = 37
Note that the first and third sequences above were generated by the polynomials n2 and n2 + 1, respectively. But what if a sequence is generated by a more complicated polynomial? Or you're tired and just not feeling very clever at the moment? How would you figure it out then?
What is the method of common differences?
The method of common differences is a process for finding a polynomial rule for a sequence.
- You write the terms of the sequence in a row, and subtract consecutive terms, listing the "differences" below and between the pairs of terms, forming a second row.
- If all of the subtractions give you the same value, you have shown the sequence to have a modelling polynomial of degree 1. If the values in this row are not the same, then repeat the process, creating a third row of differences. Continue until you get all the same values in a row, or until the last row has only one value.
- The number of rows below the original sequence row is equal to the power of the modelling polynomial.
- Create the generic polynomial for that power; for example, two rows would mean a degree-two, or quadratic, polynomial, with general form an2 + bn + c.
- Form a system of equations, using the values from the original sequence, creating one more equation than the degree of the polynomial.
- Solve the system of equations to find the coefficients of the polynomial rule for the sequence.
Let me demonstrate this process by using the last sequence above, where we already know what the answer is.
- Find the next number in the following sequence: 2, 5, 10, 17, 26,...., and provide a formula for the n-th term.
To find the pattern, I will list the numbers, and find the differences for each pair of numbers. That is, I will subtract the numbers in pairs (the first from the second, the second from the third, and so on), like this:
Since these values, called the "first differences", are not all the same value, I'll continue subtracting to form a third row:
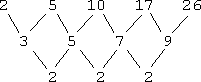
Since these values, called the "second differences", are all the same value, I can now stop.
It isn't important what the second difference is (in this case, 2); what is important is that the second differences are the same, because this tells me that the polynomial for this sequence of values is a quadratic. (Once you've studied calculus, you'll be able to understand why this is so. For now, just trust me that this works.) Since the formula for the terms of this sequence is a quadratic, then I know that it is of the form:
an2 + bn + c
...for some numbers a, b, and c. Now I have to find those numbers. How? By plugging in some of the values from the sequence, and then solving the resulting system of equations. For instance, I know that the first term (that is, the term when n = 1) is 2, so I'll plug in 1 for n and 2 for the resultin value:
a(1)2 + b(1) + c
a + b + c = 2
The second sequence term (that is, the term when n = 2) is 5, so:
a(2)2 + b(2) + c
4a + 2b + c = 5
The third term (that is, the term when n = 3) is 10, so:
a(3)2 + b(3) + c
9a + 3b + c = 10
This gives me a system of three equations in three unknowns, which I can solve. You can use whatever method you like, including using matrices in your graphing calculator:
(Remember that calculators suffer from round-off error. When you get a result like "1.3E−13", which represents "0.00000000000013", you should be aware that, in this context, this means "zero".)
Then a = 1, b = 0, and c = 1, so the formula is:
1n2 + 0n + 1 = n2 + 1
This is the same answer I'd gotten before, and it tells me that the sixth term is 62 + 1 = 36 + 1, which is:
next term: 37
formula: n2 + 1
© 2023 Purplemath, Inc. All right reserved. Web Design by 