Systems of Linear Equations: Definitions
Purplemath
A "system" of equations is a set or collection of equations that you deal with all together at once. Linear equations (ones that graph as straight lines) are simpler than non-linear equations, and the simplest linear system is one with two equations and two variables.
Think back to when you were first learning about two-variable linear equations, often stated in the form "y = mx + b. For instance, consider the linear equation y = 3x − 5. A "solution" to this equation was any (x, y)-point that "worked" in the equation.
Content Continues Below
So, for instance, the point (2, 1) is a solution to the equation because plugging in 2 for x returns the correct value for y, as shown below:
3x − 5 = 3(2) − 5 = 6 − 5 = 1 = y
On the other hand, the point (1, 2) is not a solution to the equation, because plugging in 1 for x leads to a value which is not the given y-value, as we can see:
3x − 5 = 3(1) − 5 = 3 − 5 = −2
Advertisement
This value, −2, is not the value of y that we were given; namely, +2. So the point cannot be a solution to the equation.
Affiliate
Of course, in practical terms, you did not find solutions to an equation by picking random points, plugging them in, and checking to see if they "work" in the equation. Instead, you picked x-values and then calculated the corresponding y-values. And you used this same procedure to graph the equation. This points out an important fact: Every point on the graph was a solution to the equation, and any solution to the equation was a point on the graph.
Now consider the following two-variable system of linear equations:
y = 3x − 2
y = −x − 6
Since the two equations above are in a system, we deal with them together at the same time. In particular, we can graph them together on the same axis system, like this:
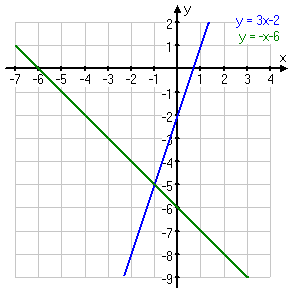
A solution for a single equation is any point that lies on the line for that equation. A solution for a system of equations is any point that lies on each line in the system. For example, the red point on the graph below is not a solution to the system, because it is not on either line:
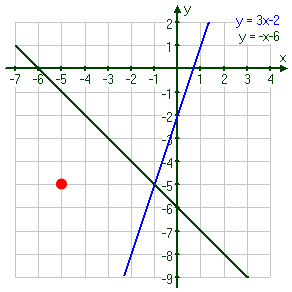
The blue point on the graph below is not a solution to the system, because it lies on only one of the lines, not on both of them:
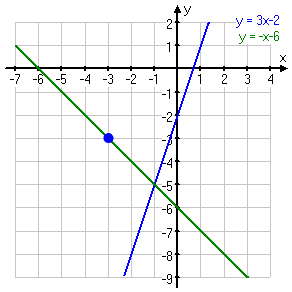
The purple point on the graph below is a solution to the system, because it does lie on both of the lines:
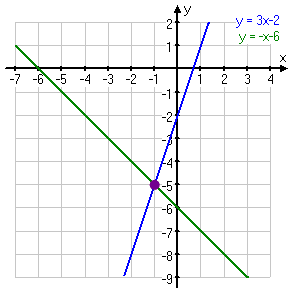
Affiliate
In particular, this purple point marks the intersection of the two lines. Since this point is on both lines, it thus solves both equations, so it therefore solves the entire system of equations.
This relationship is always true: For systems of equations, "solutions" of systems are "intersections" of lines. And you can confirm that the intersection point is the solution to the system by plugging that point back into each of the system's equations, and confirming that the point works in each equation.
Content Continues Below
Determine whether either of the points (−1, −5) and (0, −2) is a solution to the given system of equations.
y = 3x − 2
y = −x − 6
To check the given possible solutions, I just plug the x- and y-coordinates into the equations, and check to see if they work.
checking (−1, −5):
(−5) ?=? 3(−1) − 2
−5 ?=? −3 − 2
−5 = −5
(solution checks)
(−5) ?=? −(−1) − 6
−5 ?=? 1 − 6
−5 = −5
(solution checks)
Since the given point works in each equation, it is a solution to the system. Now I'll check the other point (which we already know, from looking at the graph, is not a solution):
checking (0, −2):
(−2) ?=? 3(0) − 2
−2 ?=? 0 − 2
−2 = −2
(solution checks)
So the solution does work in one of the equations. But to be a solution to the system of equations, it has to work in both of the equations in that system. Continuing the check:
(−2) ?=? −(0) − 6
−2 ?=? 0 − 6
−2 ?=? −6
But −2 does not equal −6, so this "solution" does not check. Then the answer is:
only the point (−1, −5) is a solution to the system
URL: https://www.purplemath.com/modules/systlin1.htm
You can use the Mathway widget below to practice checking if a given point is a solution to a given system. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()