|
Finding
the Next Number in a Sequence: Sections: Common differences, Recursions, General examples, Non-math "sequences" Take another look at the last sequence in the previous section:
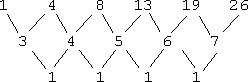
( 1/2 )(7)2 + ( 3/2 )(7) – 1 = 49/2 + 21/2 – 1 = 34 The formula we found for the terms was a bit messy, what with the fractions. But the row of first differences points out a simpler rule. Each next term was gotten by adding a growing amount to the previous term. To get the second term, they added 3 to the first term; to get the third term, they added 4 to the second term; to get the fourth term, they added 5 to the third term; and so on. The rule, in mathematical vocabulary, was "To get the n-th term, add n+1 to the (n–1)-th term." In table form, it looks like this:
This sort of sequence, where you get the next term by doing something to the previous term, is called a "recursive" sequence. In the last case above, we were able to come up with a regular formula (a "closed form expression") for the sequence; this is often not possible (or at least not reasonable) for recursive sequences, which is why you need to keep them in mind as a difference class of sequences. Probably the most famous recursive sequence is the Fibonacci sequence (pronounced "fibb - uh - NAH - chee" sequence). It is defined like this: a1
= 1 That is, the first two terms are each defined to have the value of 1. (These are called "seed" values.) Then the third term is the sum of the previous two terms, so a3 = 1 + 1 = 2. Then the fourth term is the sum of the second and the third, so a4 = 1 + 2 = 3. And so forth. The first few terms are: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,... While recursive sequences are easy to understand, they are difficult to deal with, in that, in order to get, say, the thirty-nineth term in this sequence, you would first have to find terms one through thirty-eight. There isn't a formula into which you could plug n = 39 and get the answer. (Well, there is, but its development is likely far beyond anything you've yet been trained to do.) For instance, if you try to find the differences, you'll get this:
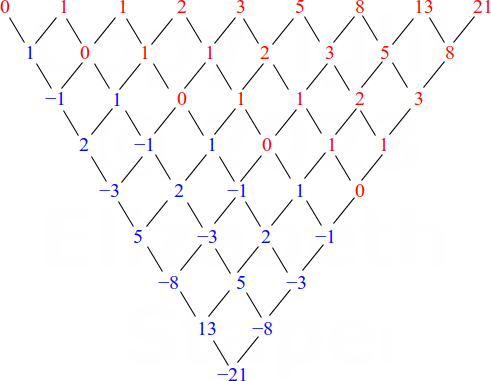
As you can see, you're not going to get a row of differences where all the entries are the same. However, you should notice that the sequence repeats itself in the lower rows, but shifted over to the right. And, in the beginning of each lower row, you should notice that a new sequence is starting: first 0; then 1, 0; then –1, 1, 0; then 2, –1, 1, 0; and so on. This is characteristic of "add the previous terms" recursive sequences. If you see this kind of behavior in the rows of differences, you should try finding a recursive formula. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved Recursive sequences can be hard to figure out, so generally they'll give you fairly simple ones of the "add a growing amount to get the next term" or "add the last two or three terms together" type:
The first two values appear to be seed values, and then I'm adding the last two terms to get the next term:
If I'm right about the rule, then the next term would be: 7 + 12 = 19 By the way, the differences look like this:
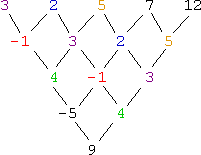
Note how the sequence terms are repeated in lower rows, but shifted to the right, and how the new sequence terms are entering from the left.
This one is harder (and is not, strictly speaking, recursive). Take a look at the differences:
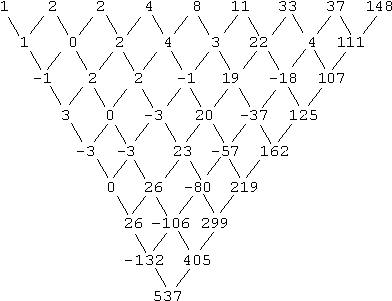
As you can see, we're getting nothing useful from this table of differences. The rule here is not consistent:
Then the next term will be "add five": 148 + 5 = 153 As the above example shows, even the table of differences might not help with a recursive sequence. But don't be discouraged if it takes a while to find a formula or a pattern. If the sequence is mathematical, then it should be possible, eventually, to find some sort of an answer. The next section demonstrates some solutions. << Previous Top | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Return to Index Next >>
|
|
|
|
Copyright © 2002-2012 Elizabeth Stapel | About | Terms of Use |
|
|
|
|
|
|
