How to Invert Rational Functions / Quarter-Circles
Defs / Inverting a GraphIs Inverse a Function?Finding InversesWorked ExamplesQuarter-CircleProving Inverses
Purplemath
Sometimes functions need to have their domains restricted, in order for the function to be invertible. On the other hand, some functions come with their own domain restrictions.
Rational functions, for example, have variables in their denominators, and their domains may therefore be restricted, in order to avoid division by zero.
Content Continues Below
These functions often have an horizontal asymptote, which usually turns out to represent a restriction on the rational function's range. (Of course, you can always check the graph, too, in order to be sure.)
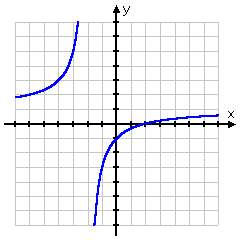
- Find the inverse of . Is the inverse a function?
First, I recognize that f (x) is a rational function. Here's its graph:
Affiliate
Advertisement
The restriction on the domain comes from the fact that I can't divide by zero, so x can't be equal to −2. I usually wouldn't bother writing down the restriction, but it's helpful here because I need to know the domain and range of the inverse.
Note from the picture (and recalling the concept of horizontal asymptotes) that y = 1 is the horizontal asymptote. Is the function ever actually equal to this value? I'll check to be sure (that it doesn't):
This is clearly false, so the function does *not* take on the value y = 1. Therefore, the domain is x ≠ −2 and the range is indeed y ≠ 1. For the inverse, they'll be swapped: the domain will be x ≠ 1 and the range will be y ≠ −2.
Now that I've sorted that out, it's time to find the inverse, starting by replacing f (x) with y:
Here's where I use a trick: I factor out the x, so then I can divide off everything that isn't x:
Since the inverse is a rational function, then, in particular, the inverse is also a function. Here's the graph of the inverse:
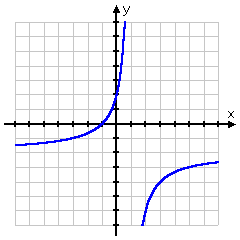
Then my answer is:
inverse:
the inverse is a function
domain: all x ≠ 1
range: all y ≠ −2
Content Continues Below
We've seen some interesting, even complicated, inverse functions. Which raises a question:
Is the inverse ever the same as the original function?
Yes, the inverse function can be the same as the original function. If the original function is symmetric about the line y = x, then the inverse will match the original function, including having the same domain and range. For instance:
- Find the inverse of
Without the domain restriction, the graph would have looked like this:
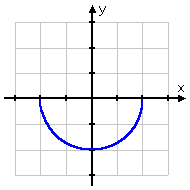
This clearly fails the Horizontal Line Test, so the inverse, without the domain restriction, would not be a function. However, with the domain restriction, I get this:
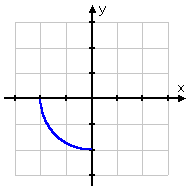
The restricted function passes the Horizontal Line Test, so now the inverse will be a function.
Since the domain of the original function is −2 ≤ x ≤ 0 and the range is −2 ≤ y ≤ 0, then the domain of the inverse will be −2 ≤ x ≤ 0 and the range will be −2 ≤ y ≤ 0. Yes, the domains and the ranges are going to be identical.
Time to find the inverse:
Since I already figured out the domain and range, I know that I have to pick the NEGATIVE square root here:
Now I switch x and y:
So the inverse is the exact same function I started with.
inverse:
domain: −2 ≤ x ≤ 0
range: −2 ≤ y ≤ 0
Affiliate
If you think about it, this makes perfect sense. The original function was one quarter of the circle centered at the origin and having radius r = 2. Considering where the reflecting line y = x goes, and the fact that the points on either side of the reflecting line are neatly symmetric, then the inverse couldn't have been anything other than what we got.
![graph of y = − sqrt[4 − x^2], -2 ≤ x ≤ 0](inverse/invers66.gif)
If you use the upper-right quarter of the circle you'll get the same result; namely, its inverse will be identical to the original function. However, if you take either of the other two quarters, you'll get the remaining quarter as the inverse:
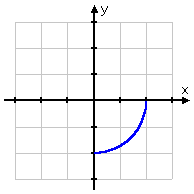 ...and:
...and: 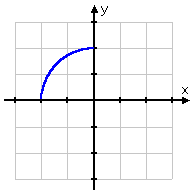
URL: https://www.purplemath.com/modules/invrsfcn5.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




