Graphing Logarithmic Functions: More Examples

Return to the Lessons Index | Do the Lessons in Order | Print-friendly page

Graphing Logarithmic Functions: Examples (page 3 of 3)

Graph y = log₂(x + 3).

This graph will be similar to the graph of log₂(x), but it will be shifted sideways.

Since the "+ 3" is inside the log's argument, the graph's shift cannot be up or down. This means that the shift has to be to the left or to the right. But which way? You can keep track of the direction of the shift by looking at the basic point (1, 0) ("basic" because it's neat and easy to remember). The log will be 0 when the argument, x + 3, is equal to 1. When is x + 3 equal to 1? When x = –2. Then the basic log-graph point of (1, 0) will be shifted over to
(–2, 0) on this graph; that is, the graph is shifted three units to the left. If you are not comfortable with this concept or these manipulations, please review how to work with translations of functions.

Since a log cannot have an argument of zero or less, then I must have x + 3 > 0, this tells me that, for this graph, x must always be greater than –3.

The graph of the basic log function y = log₂(x) crawled up the positive side of the y-axis to reach the x-axis, with the line never going to the left of the limitation that x must be greater than zero. To remind myself of the similar limitation of this log (where x must always be greater than –3), I will insert a dashed line at x = –3:

graph showing vertical asymptote at x = -3

A line like this, which marks off territory where the graph shouldn't go, is called a "vertical asymptote", or simply an "asymptote". I don't have to add this to the graph, but it can be very helpful, and might convince the grader that I know what I'm doing.

After I dash in the asymptote, I plot some points:

2⁰ = 1, so log₂(1) = 0; x + 3 = 1 for x = –2: (–2, 0)
2¹ = 2, so log₂(2) = 1; x + 3 = 2 for x = –1: (–1, 1)
2² = 4, so log₂(4) = 2; x + 3 = 4 for x = 1: (1, 2)
2³ = 8, so log₂(8) = 3; x + 3 = 8 for x = 5: (5, 3)

2^–1 = 0.5, so log₂(0.5) = –1;
        x + 3 = 0.5 for x = –2.5: (–2.5, –1)
2^–2 = 0.25, so log₂(0.25) = –2;
        x + 3 = 0.25 for x = –2.75: (–2.75, –2)
2^–3 = 0.125, so log₂(0.125) = –3;
        x + 3 = 0.125 for x = –2.875: (–2.875, –3)

Note that, to find each of these points, I did not start with an x-value and then puzzle my way to a y-value; that would be too hard, and I'm too lazy. Instead, I started with a simple exponential statement, switched it around to the corresponding logarithmic statement, and then figured out, for that exponent (which is also my y-value), what the x-value needed to be. This method is, in my view, much the simpler way to work these problems.

Plotting the points I've calculated, I get:

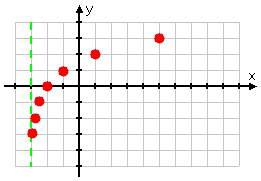
graph showing plotted points

...and connecting the dots gives me the following graph:

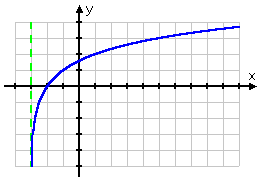
graph of y = log_2(x + 3)

If you check this in your calculator, first, remember to put the "x + 3" inside parentheses, or your calculator will think you mean "log₂(x) + 3", and you'll get the wrong answer; second, remember that your calculator can only follow its programming — it can't think — so the graph it displays will likely be incorrect, even if you enter the function correctly.

If you plug y = log₂(x + 3) into a graphing calculator (in the change-of-base formulation of "ln(x + 3) / ln(2)"), you will likely get a graph that looks something like this:

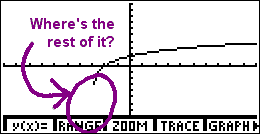
screen-capture of y = ln(x + 3)/ln(2)

Now, you know full well that the log doesn't just "end" there at the left, hanging uselessly in space. Why is the calculator doing it wrong? Because it's just a machine, and it's doing the best it can. The calculator graphs in a manner similar to how you do: it picks x-values, computes y-values, plots the points, and connects the dots. But, whereas you know that the log graph continues downward forever, getting infinitesimally close to the y-axis (or whatever the vertical asymptote happens to be), the calculator only knows that it tried one x-value on its list, got "ERROR" for an answer, tried the next x-value on its list, and got a valid y-value. Since it has no other dots before that first one, and because it can't think, it starts the graph with that first dot. This is another instance of "student smart; calculator stupid". Don't assume, just because the calculator displays a graph a certain way, that this is what the graph actually looks like. Use your head!

To review: below are some different variations on the same basic logarithmic function, with the associated graph below each equation. Note that, even if the graph is moved left or right, or up or down, or is flipped upside-down, it still displays the same curve:

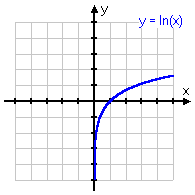
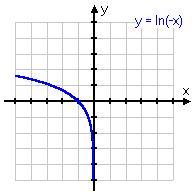
y = ln(x)	y = ln(–x)	y = –ln(x)

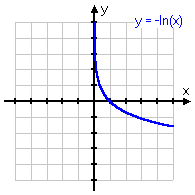
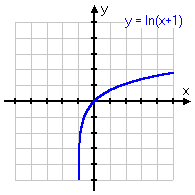
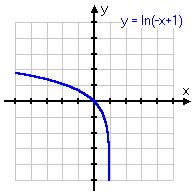
y = ln(x + 1)	y = ln(–x + 1)	y = –ln(–x)

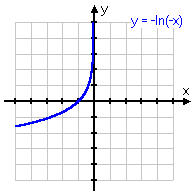
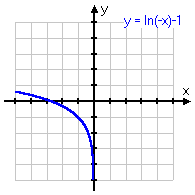
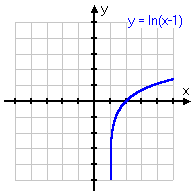
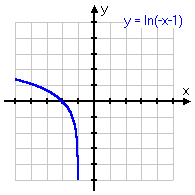
y = ln(x) – 1	y = ln(–x) – 1	y = ln(x – 1)

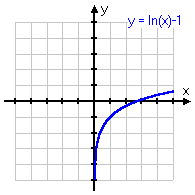
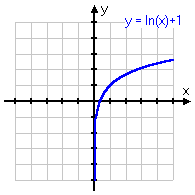
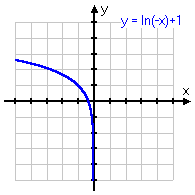
y = ln(x) + 1	y = ln(–x) + 1	y = ln(–x – 1)