Finding General Polynomials from Their Zeroes
Purplemath
To find a quadratic (that is, a degree-two polynomial) from its zeroes or roots, we convert the statement that x = a is a zero to the fact that x − a must then have been a factor. We can use these zeroes to find the general form of the quadratic.
And if we're given another point on the graph, we can use this to determine the exactly one quadratic that they'd had in mind.
How about if they give you more than just one or two roots? Then your answer will be a polynomial of degree higher than 2. But the process for finding polynomials from their zeroes works the same as for finding quadratics from their zeroes.
You know that any nice neat whole-number or fractional root turns into a nice neat linear factor. And any messy root with a square root or a complex number in it turns into a paired root. Using this knowledge, you can find the corresponding polynomial.
What are the steps for finding a polynomial from its zeroes?
- Take the roots they give you.
- Create all of your factors from these roots.
- Multiply together all of these factors.
- Finish by doing one of the following:
- Either tack on the "I don't know if you divided something out" constant a,
- Or else use the extra point they give you to solve for the value of a.
What is an example of finding a polynomial from its roots?
- Find the polynomial with integer coefficients having roots at 3, −5, and −½, and passing through (−1, 16).
To find the factors, I subtract the roots, so my factors are x − 3, x − (−5) = x + 5, and x − (−½) = x + ½. To find the general form of the polynomial, I multiply the factors:
(x − 3)(x + 5)(x + ½)
= (x2 + 2x − 15)(x + ½)
= x3 + 2.5x2 − 14x − 7.5
This polynomial has decimal coefficients, but I'm supposed to be finding a polynomial with integer coefficients. So I'll first multiply through by 2 to get rid of the fractions:
2(x3 + 2.5x2 − 14x − 7.5)
= 2x3 + 5x2 − 28x − 15
Then my general form of the polynomial is a(2x3 + 5x2 − 28x − 15). Plugging in the point they gave me, I get:
a(2x3 + 5x2 − 28x − 15) = y
a((2(−1)3 + 5(−1)2 − 28(−1) − 15) = 16
a(−2 + 5 + 28 − 15) = 16
a(16) = 16
a = 1
It doesn't often happen with this type of problem, but sometimes a will turn out to be 1, in which case nothing more needs to be done. The polynomial they're looking for is:
2x3 + 5x2 − 28x − 15
- Find the polynomial having rational coefficients and having roots at −1, and 4, and passing through (3, −4).
Two of the factors are easy to find. If I have zeroes at x = −1 and x = 4, then I must have factors of x − (−1) = x + 1 and x − 4.
The other solution is messy, what with the square root in it. Since they specified that the polynomial has rational (that is, fractional or integer) coefficients, I know I can't leave that square root by itself; I have to find its pair that the Quadratic Formula created.
In the Quadratic Formula, the ± symbol is right in front of the square root, so the pair for the solution must be .
(Warning: The pair to the given root is *not* or . Be careful with that sign change; the sign change occurs only between the two terms, right in front of the square-root part. No other sign changes.)
Then the remaining factors are and .
When I go to multiply my factors together, I'm going to multiply these messy factors first. It can be very helpful to do this multiplication work "vertically", the way you probably learned back when you studied how to multiply polynomials.
Note: You can check that this multiplication is correct by solving " x2 − 4x + 1 = 0 " in the Quadratic Formula, and verifying that the solutions are indeed and .
Now I multiply in the other factors:
(x2 − 4x + 1)(x + 1)(x − 4)
= (x2 − 4x + 1)(x2 − 3x − 4)
= x4 − 7x3 + 9x2 + 13x − 4
Then the general form is a(x4 − 7x3 + 9x2 + 13x − 4). To solve for that constant, I'll plug in the point they gave me:
a(x4 − 7x3 + 9x2 + 13x − 4) = y
a((3)4 − 7(3)3 + 9(3)2 + 13(3) − 4) = −4
a(81 − 189 + 81 + 39 − 4) = −4
a(8) = −4
a = −0.5
Then the polynomial they started with was:
−0.5(x4 − 7x3 + 9x2 + 13x − 4)
You can check your work by doing a quick graph. If the x-intercepts of your polynomial match the (real) zeroes they gave you and the given point is on the graph (or displayed in the TABLE of values), then you know your answer is correct.
entering the polynomial into the calculator
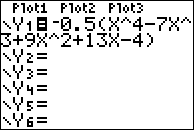
checking the graph: all the roots are there
verifying: the point is listed as being on the graph
If they give you a complex root, the pairing process for finding the remaining roots works the same way, because you know that complexes are generated by negatives inside the square root in the Quadratic Formula. (You can't check the complex roots on a graph, of course, since complex roots don't graph as x-intercepts. But you can still confirm the real roots.)
What is an example of finding a polynomial from its complex roots?
- Find the polynomial having roots at −2i and 3 + i, and passing through (3, −13).
The complex roots are generated in pairs, so the full listing of the roots will be −2i, 2i, 3 + i, and 3 − i. (Note how I only changed the sign on the part of the root that came from the square root in the Quadratic Formula.)
Then the factors were x − (−2i) = x + 2i, x − 2i, x − (3 + i) = x − 3 − i, and x − (3 − i) = x − 3 + i. Since the Quadratic Formula spits the roots out in pairs, it's generally easiest to multiply the roots back together in pairs. Here's the first multiplication:
And here's the second multiplication:
Multiplying pairs of factors gave me two polynomials, each of which is a factor of whatever was the original polynomial (namely, the polynomial that I need to find). To get the entire polynomial, I need to multiply these two polynomials together. When I do so, I get:
(x2 − 6x + 10)(x2 + 4)
= x4 − 6x3 + 14x2 − 24x + 40
This is the polynomial before I check whether there was a number divided out of each of the terms of the original polynomial. Using the extra point they gave me, I plug the coordinates into the equation, and solve for the value of any numerical factor of the original polynomial:
a( x4 − 6x3 + 14x2 − 24x + 40 ) = −13
a((3)4 − 6(3)3 + 14(3)2 − 24(3) + 40) = −13
a(81 − 162 + 126 − 72 + 40) = − 13
a(13) = −13
a = −1
Then the desired polynomial is:
−x4 + 6x3 − 14x2 + 24x − 40
That's all there is to this topic. You take the roots they give you, and subtract each of them from x; this gives you your factors. If you have a messy root (with a square root or a complex number), you create the paired root, and subtract it from x too. Multiply all your factors together, starting with any messy pairs first. Then you either multiply the whole thing by some generic "I don't know if you divided something off" constant a, or, if they give you an extra point on the curve, you solve for the value of the multiplier a.
About the only mistake students make in this process is in forming the factors: always remember to subtract the zeroes from x; don't add them. And remember that you can always check your work by setting your polynomial answer equal to zero and finding the roots. As long as your solutions match the ones you were given in the first place, you must be at least close to the right answer.
© 2022 Purplemath, Inc. All right reserved. Web Design by 