Even and Odd Functions
Purplemath
What are even and odd functions (in math)?
An even function is one whose graph exhibits symmetry about the y-axis; an odd function is one whose graph exhibits symmetry about the origin. Which is a fancy way of saying that, if you split the graphs down the middle at the y-axis, an even function's halves will mirror each other exactly, while an odd function's halves with be upside-down of each other.
Content Continues Below
How do you determine, algebraically, if a function is even, odd, or neither?
Advertisement
In order to "determine algebraically" whether a function is even, odd, or neither, you take the function and plug −x in for x, simplify, and compare the results with what you'd started with.
If you end up with the exact same function that you started with (that is, if f (−x) = f (x), so all of the signs are the same), then the function is even; if you end up with the exact opposite of what you started with (that is, if f (−x) = −f (x), so all of the signs are switched), then the function is odd.
If the result is neither exactly the same nor exactly opposite (that is, if the result has neither all the same terms nor all the same terms but with opposite signs), then the function is neither even nor odd. Most functions, in fact, will be neither even nor odd.
What is an example of determining if a function is even, odd, or neither?
- Determine algebraically whether f (x) = −3x2 + 4 is even, odd, or neither.
If I graph this, I will see that this is "symmetric about the y-axis"; in other words, whatever the graph is doing on one side of the y-axis is mirrored exactly on the other side:
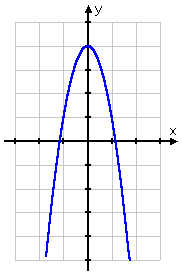
This mirroring about the y-axis is a hallmark of even functions.
Also, I note that the exponents on all of the terms are even — the exponent on the constant term being zero: 4x0 = 4 × 1 = 4. These are helpful clues that strongly suggest to me that I've got an even function here.
But the question asks me to make the determination algebraically, which means that I need to do the actual algebra.
So I'll plug −x in for x, and simplify:
f (−x) = −3(−x)2 + 4
= −3(x2) + 4
= −3x2 + 4
I can see, by comparing the original function with my final result above, that I've got a match, which means that:
f (x) is even
Affiliate
-
Determine algebraically whether f (x) = 2x3 − 4x is even, odd, or neither.
If I graph this, I will see that it is "symmetric about the origin"; that is, if I start at a point on the graph on one side of the y-axis, and draw a line from that point through the origin and extending the same length on the other side of the y-axis, I will get to another point on the graph.
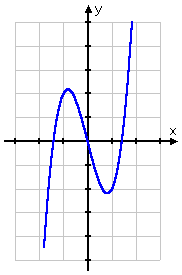
If that description doesn't make much sense to you (and it didn't make much sense to me), you can also think of this kind of symmetry as the half of the graph on one side of the y-axis being the upside-down version of the half of the graph on the other side of the y-axis. This symmetry is a hallmark of odd functions.
Note also that all the exponents in the function's rule are odd, since the second term can be written as 4x = 4x1. This is a useful clue. I should expect this function to be odd.
The question asks me to make the determination algebraically, so I'll plug −x in for x, and simplify:
f (−x) = 2(−x)3 − 4(−x)
= 2(−x3) + 4x
= −2x3 + 4x
For the given function to be odd, I need the above result to have all opposite signs from the original function. So I'll write the original function, and then switch all the signs:
original: f (x) = 2(x)3 − 4(x)
switched: ⚊f (x) = ⚊2x3 + 4x
Comparing this to what I got, I see that they're a match. When I plugged −x in for x, all the signs switched. This means that, as I'd expected:
f (x) is odd.
Content Continues Below
- Determine algebraically whether f (x) = 2x3 − 3x2 − 4x + 4 is even, odd, or neither.
This function is the sum of the previous two functions. But, while the sum of an odd and an even number is an odd number, I cannot conclude the same of the sum of an odd and an even function.
Note that the graph of this function does not have the symmetry of either of the previous ones:
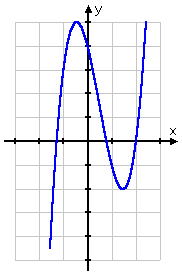
...nor are all of its exponents either even or odd. Two terms are even; two are odd.
Based on the exponents as well as the graph, I would expect this function to be neither even nor odd. To be sure, though (and in order to get full credit for my answer), I'll need to do the algebra.
I'll plug −x in for x, and simplify:
f (−x) = 2(−x)3 − 3(−x)2 − 4(−x) + 4
= 2(−x3) − 3(x2) + 4x + 4
= −2x3 − 3x2 + 4x + 4
I can see, by a quick comparison, that this does not match what I'd started with, so this function is not even. What about odd?
To check, I'll write down the exact opposite of what I started with, being the original function, but with all of the signs changed:
⚊f (x) = ⚊2x3 + 3x2 + 4x + 4
This doesn't match what I came up with, either. So the original function isn't odd, either. Then, as I'd expected:
f (x) is neither even nor odd.
Affiliate
As you can see, the sum or difference of an even and an odd function is not an odd function. In fact, you'll discover that the sum or difference of two even functions is another even function, but the sum or difference of two odd functions is another odd function.
Is there any function that is both even *and* odd?
There is (exactly) one function that is both even and odd; it is the zero function, f (x) = 0.
In other words, "even" and "odd", in the context of functions, mean something every different from how these terms are used with whole numbers. Don't try to mix the two sets of definitions; it'll only confuse you.
Just because all of the examples so far have involved polynomial functions, don't think that the concept of even and odd functions is restricted to polynomials. It's not. Trigonometry is full of functions that are even or odd, and other types of functions can come under consideration, too.
- Determine whether is even, odd, or neither.
This is a rational function. The process for checking if it's even, odd, or neither is the same as always. I'll start by plugging −x in for x:
I can see, by comparison, that this is the same as what I'd started with. So:
g(x) is even
You may find it helpful, when answering this "even or odd" type of question, to write down −f (x) explicitly, and then compare this to whatever you get for f (−x). This can help you make a confident determination of the correct answer.
You can use the Mathway widget below to practice figuring out if a function is even, odd, or neither. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Clicking on "Tap to view steps" on the widget's answer screen will take you to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/fcnnot3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



