Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Graphing Rational Functions: Introduction (page 1 of 4)

Sections: Introduction, Examples, The special case with the "hole"

To graph a rational function, you find the asymptotes and the intercepts, plot a few points, and then sketch in the graph. Once you get the swing of things, rational functions are actually fairly simple to graph. Let's work through a few examples.

  • Graph the following:

      • y = (2x + 5) / (x - 1)

    First I'll find the vertical asymptotes, if any, for this rational function. Since I can't graph where the function doesn't exist, and since the function won't exist where there would be a zero in the denominator, I'll set the denominator equal to zero to find any forbidden points:

      x – 1 = 0
      x = 1

     

     

    So I can't have x = 1, and therefore I have a vertical asymptote there.

    I'll dash this in on my graph:

      

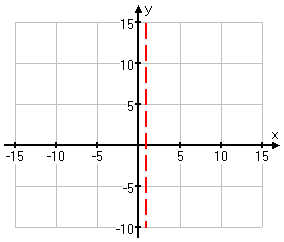
    graphing showing vertical asymptote at x = 1

    Next I'll find the horizontal or slant asymptote. Since the numerator and denominator have the same degree (they're both linear), the asymptote will be horizontal, not slant, and the horizontal asymptote will be the result of dividing the leading coefficients:

      y = 2/1 = 2

     

     

    I'll dash this in, too:

      

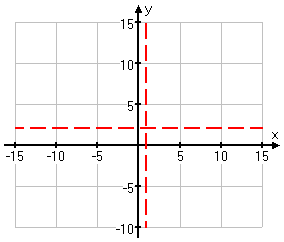
    graph showing horizontal asymptote at y = 2

    (If you're not sure of how I found these asymptotes, then review the lesson on asymptotes.  You will need to be comfortable with this topic before you proceed further with graphing rationals.)

    Next, I'll find any x- or y-intercepts.

      x = 0:  y = (0 + 5)/(0 – 1) = 5/–1 = –5
      y = 0:  0 = (2x + 5)/(x – 1)
                          0 = 2x + 5
              –5 = 2x
                 –2.5 = x

     

     

    Then the intercepts are at (0, –5)
    and (–2.5, 0). I'll sketch these in:

      

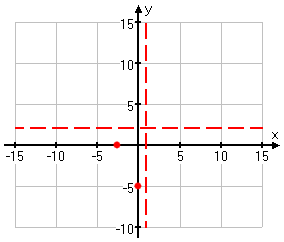
    graphing showing x- and y-intercepts

    Now I'll pick a few more x-values, compute the corresponding y-values, and plot a few more points.   Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

      x

      y = (2x + 5)/(x – 1)
      –6

      (2(–6) + 5)/((–6) – 1) = (–12 + 5)/(–7) = (–7)/(–7) = 1
      –1 (2(–1) + 5)/((–1) – 1) = (–2 + 5)/(–2) = (3)/(–2) = –1.5
      2 (2(2) + 5)/((2) – 1) = (4 + 5)/(1) = (9)/(1) = 9
      3 (2(3) + 5)/((3) – 1) = (6 + 5)/(2) = (11)/(2) = 5.5
      6 (2(6) + 5)/((6) – 1) = (12 + 5)/(5) = (17)/(5) = 3.4
      8 (2(8) + 5)/((8) – 1) = (16 + 5)/(7) = (21)/(7) = 3
      15 (2(15) + 5)/((15) – 1) = (30 + 5)/(14) = (35)/(14) = 2.5

    I mostly picked x-values near the middle of the graph: because of the horizontal asymptote, I already have a good idea of what the graph does off to the sides. (It can be a good idea to do a point or two near the ends anyway, as a check on your work.) Also, since I had no intercepts on the right-hand side of the vertical asymptote to give me hints as to what was happening with the graph, I needed more points there to show me what was going on.

      

      

    Now I'll plot these points:

      

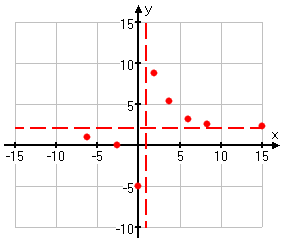
    graph with T-chart points plotted
      

      

      

    And now I can connect the dots:

      

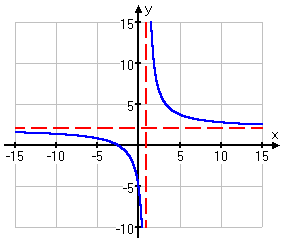
    graph of y = (2x + 5) / (x - 1)

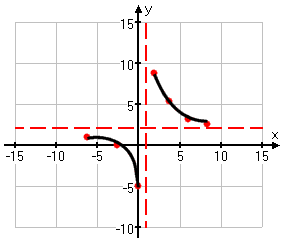
When you draw your graph, make sure you show the graph continuing off to the sides.

 

 

Don't just stop at a point you've drawn, because this will make it look as though the graph actually stops at that point.

  
DON'T DO THIS!
Don't draw your graph like this!

Warning: Your calculator may display a misleading graph for a given rational function. When you graph, you plot some points and then you connect them. Your calculator does the same thing. But you're smart enough to know not to cross a vertical asymptote. Your calculator isn't that intelligent.

  
If your calculator shades a pixel down at the bottom of the screen, and then the next computed pixel to be shaded is at the top of the screen, then the calculator is likely to merrily draw a nice vertical line connecting the two dots, like this:

  

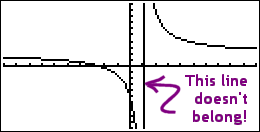
The calculator draws an extra line that doesn't belong.
  

  
For this reason, you may wish to switch your graphing mode from "line" to "dot" (or the equivalent setting for your calculator model; check your owner's manual). In "dot" mode, you'll get a graph that looks like this:

  

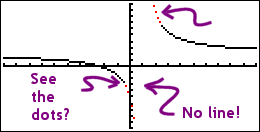
'dot' mode can be hard to read, but you don't get extra lines.

I've highlighted the disconnected dots in red. The whole graph is dots, but most of the dots are right next to each other, so they look like a line. If you keep the graphing mode as "line", you will need to remember that what the screen displays may be somewhat incorrect when graphing rationals.

Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Graphing Rational Functions: Introduction." Purplemath. Available from
    https://www.purplemath.com/modules/grphrtnl.htm. Accessed
 

 

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

   Copyright © 2021  Elizabeth Stapel   |   About   |   Terms of Use   |   Linking   |   Site Licensing

 

Contact Us