Complex Numbers and the Quadratic Formula
Purplemath
For the time being, you will probably be using complex numbers only in the context of solving quadratic equations for their zeroes. (There are many other practical uses for complexes, but you'll have to wait for more interesting classes like "Engineering 201" to get to the good stuff.) So let's refresh on the topic.
The Quadratic Formula takes the generic quadratic equation, stated as:
ax2 + bx + c = 0
Content Continues Below
...and provides the solution values of the variable x by plugging the values a, b, and c of the numerical coefficients into the following formula:
Previously, when the Formula gave you a negative value inside the square root (that is, inside the "discriminant"), you would have responded that the equation under question had "no solutions". Were you to graph the quadratic equation (setting the quadratic equal to y instead of to 0), your graph would not cross the horizontal axis.
Affiliate
Advertisement
Now, with complex numbers, when the Formula gives you a negative inside the root, you now can simplify that solution by using the imaginary and respond that the equation under question has no real-valued solution, but it does have a complex-valued solution. Were you to graph the quadratic equation, your graph will still not cross the horizontal axis.
The difference now is that you have solutions (from the Quadratic Formula) to the equation which are not graphable. "Solutions", "roots", and "zeroes" of a given quadratic equation are now no longer necessarily also "x-intercepts".
The values on the x,y-plane are real numbers, so the complex-valued solutions of the equation cannot be seen on the x-axis. Your complex-valued answer is still a valid "zero" or "root" or "solution" for that quadratic equation, because, if you plug the answer value back into the quadratic equation, you'll get zero after you simplify. (This is the definition of a "solution"; it is a value that solves the equation, making it true.) However, this complex-valued answer will not be a graphable x-intercept of the graph.
What is the connection between the Quadratic Formula, complex numbers, and graphing?
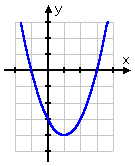
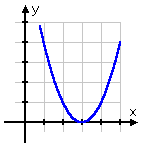
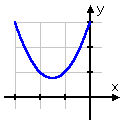
The connection between the Quadratic Formula, complex numbers, and graphing is illustrated in the table below:
x2 − 2x − 3 |
x2 − 6x + 9 |
x2 + 3x + 3 |
|---|---|---|
a positive number inside the square root |
zero inside the square root |
a negative number inside the square root |
two real solutions |
one (repeated) real solution |
two complex solutions |
|
|
|
two distinct x-intercepts |
one (repeated) x-intercept |
no x-intercepts |
Content Continues Below
In the discussion above, I repeatedly pointed out that complex solutions to a quadratic equation are not graphable in the x,y-plane, because all points on the x,y are pairs of real numbers. However, if we change what the axes stand for, we can plot complex numbers.
How can you graph complex numbers?
To graph a complex number, you:
- Draw the regular x,y-plane.
- Label the axes:
- using the regular x and y labels
- using the regular x for the horizontal axis, but use yi for the vertical axis
- using "Re" for the horizontal axis having real-number values, and using "Im" for the vertical axis having imaginary-number values
- Convert the complex number from "a + bi" summing (that is, additive) form to "(a, b) coordinate form
- Plot the point just as you would a coordinate point on the coordinate plane
For instance, you would plot the complex number 3 − 2i by converting the complex number into coordinate-point form (that is, into (3, −2) form), and then graphing in the usual way: starting at the origin, moving three units to the right along the x-axis, moving two units down parallel to the y-axis, and drawing a dot. Here's what it looks like:

Affiliate
This graphability of complex numbers leads somewhere interesting.
When you learned about regular (that is, about "real") numbers, you also learned about their order on the number line. But x,y-points don't come in any particular order. You can't say that one point "comes after" another point in the same way that you can say that one number comes after another number; you can't say that (4, 5) "comes after" (4, 3) in the way that you can say that 5 comes after 3.
Pretty much all you can do is compare the "sizes" of the different points, and, for complex numbers as for regular x,y-points, "size" means "how far from the origin". To find a point's size, you use the Distance Formula. Complexes that are closer to the origin will have smaller sizes; complexes further away will have larger values.
This "size" concept is called "the modulus" of a complex-valued point. For instance, the modulus of the above-graphed point (denoted by absolute-value bars around the absolute-value bars) is computed by using the Distance Formula:
Note that all points at this distance from the origin have the same modulus. All the points on the circle with radius are also the set of all complex numbers having the same "size" as 3 − 2i. So this is another compromise we've had to make: in getting the imaginary i and the ability to deal with negatives inside square roots, we have lost the absolute-ness of distance. While only and exactly one point on the number line can be, say, five units to the right of zero, there are infinitely-many complex numbers that can be five units away from the double-zero that is the origin. We lose uniqueness.
Now, isn't that interesting? 😎
URL: https://www.purplemath.com/modules/complex3.htm
You can use the Mathway widget below to practice finding the magnitude (or modulus or "size") of complex numbers. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()