Complex Fractions: More Examples
Purplemath
The complex fractions just keep coming, and some of them come with surprises. Let's dig in!
- Simplify the following complex fraction:
Can I start my simplification by hacking off the x − 3's? Can I cancel the 4 with the 12? Or any of the 3's with the 9 or the 12? (Hint: Really, sincerely, no!)
Content Continues Below
The common denominator for this complex fraction is x − 3, so I'll multiply through, top and bottom, by that.
Clearly, nothing else cancels, so my final answer is:
Affiliate
Advertisement
It is highly unusual for a complex fraction to simplify as much as the above fraction did, but obviously it *can* happen.
In this case, the "except for x equal to 3" part is rather important, since it is not at all apparent (at the start) that the original fraction is (almost always) equal to . Indeed, the original fraction is not even defined for x equal to 3 (since this would cause division by zero). If the original expression had been set equal to y and the instructions on the exercise had been to graph the function, the result would have been the graph of a straight line with a hole; the line would have been horizontal at a height of three-fourths of a unit above the x-axis, with an open hole at x = 3.
By the way, those with sharp eyes may notice something about the above exercise that I'd missed; namely, it was possible to factor out in the first step, and cancel to get the answer right away. This would have looked like the following:
The only downside of the above cleverness is that it is harder to locate the forbidden values of the variable, because there was no step at which an x was cancelled off. While the one restriction (namely, x ≠ 3, from the denominators in the smaller fractions) is clear from the beginning, the second restriction is not obvious. In such a case, one has to find the value(s) of the variable which would cause the denominator of the entire stacked fraction to be zero (because this would cause division by zero for the stacked fraction). In the above case, this process would be the following:
Yes, complex fractions can be messy and involved.
Content Continues Below
- Simplify the following complex rational expression:
Can I start my simplification by canceling multiplications with additions, or between the numerator of one fraction and the denominator of another fraction to which it is added (rather than multiplied), as shown below?
DON'T DO THIS!
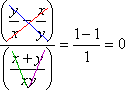
NOT EVER!
I can only cancel factors within the same fraction, not terms or portions of different added fractions, so the above cancellations are not in any way proper.
Instead, the first thing I will do is multiply through, top and bottom, by the common denominator of xy.
Then my final answer is:
y − x, for x, y ≠ 0, x ≠ −y
- Simplify the following expression:
Can I start by canceling off the 1's or the 1/t's? (Hint: Still really no!)
I first note that the variable cannot equal zero, as this would cause division by zero. Moving on, I multiply through, top and bottom, by the common denominator of t.
Affiliate
Can I reach inside the "understood" parentheses that enclose the polynomial expressions in the numerator and denominator, and cancel off just the t's now? Or cancel off just the 1's? (Hint: Still and forever, no!)
I can only cancel factors, not terms inside larger expressions. Therefore I've reached the point at which there is nothing left that factors; this is as simplified as it gets. Then my final hand-in answer is:
Methods and techniques are helpful but, even having those, there are more important take-aways:
- When you're working with complex fractions, take the time to show each step completely. (Do yourself the *favor* of giving yourself the time to take!)
- Don't try to skip steps or do everything (or even much of anything) in your head.
- Don't get careless with cancellation: remember that you can only cancel factors, not terms that are parts of larger expressions.
Do I follow these steps, too? Yes!
If you keep these things straight and do your work clearly, you should be fairly successful with these problems. Just don't rush; give yourself time for familiarity to grow.
By the way, sometimes the following questions are asked:
How do you solve complex fractions?
Complex fractions are expressions, which can be evaluated, simplified, rearranged, etc. But it's only equations that can be solved. Since there is no "equals" sign inside a complex fraction, there is nothing to solve. Yes, there are variables; no, you can't solve for their values. Not until you're given a rational equation is there anything that can be solved.
What is the rule for simplifying complex fractions?
There is no one rule for simplifying complex fractions. Instead, there are two methods, and the only rule is to use the method that you have found works better for you.
URL: https://www.purplemath.com/modules/compfrac2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()