Quartiles, Boxes, and Whiskers
Purplemath
For many computations in statistics, it is assumed that your data points (that is, the numbers in your list) are clustered around some central value; in other words, it is assumed that there is an "average" of some sort.
The "box" in the box-and-whisker plot contains, and thereby highlights, the middle portion of these data points.
Content Continues Below
How to create a box-and-whisker plot
To create a box-and-whisker plot, we follow just a few simple steps:
- List the data points in numerical order, smallest to greatest.
- Find the median of the listed values. Name this value Q2.
- Find the median of each of the lower and upper halves of the data. Name these values Q1 and Q3, respectively.
- On an appropriately-labelled graph, draw line segments marking the smallest value in the data set, the largest value, and the three values Q1, Q2, and Q3.
- Join the ends of the segments for Q1 and Q3, forming a box with Q2 inside of the box. (This is the "box" from the name for this plot.)
- From the center of the segment for Q1, draw a line to the segment for the smallest data point; draw another line from Q3 to the segment for the largest point. (These are the "whiskers" from the name for this plot.)
Note: If we have an even number of values, so the first median was the average of the two middle values, then we include the middle values in our sub-median computations (that is, in our computations for Q1 and Q3). If we have an odd number of values, so the first median was an actual data point, then we do not include that value in our sub-median computations. That is, to find the sub-medians with an odd number of values in our list, we only look at the values that have not yet been used.
So we have five points: the first middle point (the median), the middle points of the two halves (what I've been calling the sub-medians), and the smallest and largest values in the list. These five points mark the data set into quarters, called "quartiles". (These quarters are not one-fourths; I'm using the term "quarters" very loosely here.)
Affiliate
Once we have found these five points — the smallest value, Q1, Q2, Q3, and the largest value — we have all we need in order to draw a simple box-and-whisker plot. Here's an example of how it works.
- Draw a box-and-whisker plot for the following data set:
4.3, 5.1, 3.9, 4.5, 4.4, 4.9, 5.0, 4.7, 4.1, 4.6, 4.4, 4.3, 4.8, 4.4, 4.2, 4.5, 4.4
My first step is to order the values in this set of numbers, going from least to greatest. This gives me the following ordered list:
3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4, 4.4, 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
The first value I need to find from this ordered list is the median of the entire set. Since there are seventeen values in this list, the ninth value is the middle value of the list, and is therefore my median:
3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4, 4.4, 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4, 4.4, 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
The median is Q2 = 4.4
The next two numbers I need are the medians of the two halves. Since I used the "4.4" in the middle of the list, I can't re-use it, so my two remaining data sets are:
3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4
...and:
4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1
The first half has eight values, so the median is the average of the middle two values:
Q1 = (4.3 + 4.3) ÷ 2 = 4.3
The median of the second half is:
Q3 = (4.7 + 4.8) ÷ 2 = 4.75
To draw my box-and-whisker plot, I'll need to decide on a scale for my measurements. Since the values in my list are written with one decimal place and range from 3.9 to 5.1, I won't use a scale of, say, zero to ten, marked off by ones. Instead, I'll draw a number line from 3.5 to 5.5, and mark off by tenths.
(You might choose to measure from, say, 3 to 6. Your choice would be as good as mine. The idea here is to be "reasonable", which allows you some flexibility; and to label clearly, so the grader knows what you mean.)
Now I'll mark off the minimum and maximum values, and Q1, Q2, and Q3:
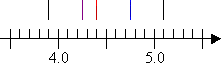
The "box" part of the plot goes from Q1 to Q3, with a line drawn inside the box to indicate the location of the median, Q2:
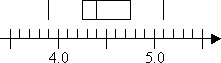
And then the "whiskers" are drawn to the endpoints:
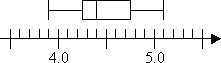
By the way, box-and-whisker plots don't have to be drawn horizontally as I did above; they can be vertical, too.
Content Continues Below
As mentioned at the beginning of this lesson, the "box" contains the middle portion of your data. As you can see in the graph above, the "whiskers" show how large is the "spread" of the data.
If you've got a wide box and long whiskers, then maybe the data doesn't cluster as you'd hoped (or at least not as you'd assumed). If your box is small and the whiskers are short, then probably your data does indeed cluster. If your box is small and the whiskers are long, then maybe the data clusters, but you've got some "outliers" that you might need to investigate further — or, as we'll see later, you may want to discard some of your results.
- Draw the box-and-whisker plot for the following data:
98, 77, 85, 88, 82, 83, 87
My first step is to order the data:
77, 82, 83, 85, 87, 88, 98
Next, I'll find the median. This set has seven values, so the fourth value is the median:
Q2 = 85
The median splits the remaining data into two sets. The first set is 77, 82, 83. The median of this set is:
Q1 = 82
The other set is 87, 88, 98. The median of this set is:
Advertisement
Q3 = 88
I now have all the values I need for my box-and-whisker plot. Next, I need to figure out what sort of scale I'll use for this.
Since all the values are two-digit whole numbers, I won't bother with decimal places. Because the extreme values (that is, the smallest and largest values) are 77 and 98 (twenty-two units apart), I'll use 75 to 100 for min and max values, and I'll count by two's for my scale.
(There's nothing special about these values; they're just what feel reasonable to me at the time of writing. Your choices may differ. Just don't go using something silly like 50 to 150 or 76.5 to 98.1.)
My set-up looks like this:

The crooked portion at the bottom of the vertical axis indicates that there is a portion of the number-line that's been omitted. In other words, this notation makes clear that the units for the vertical axis do not start from zero.
Affiliate
(This zig-zag portion of the axis appears generally to go by the name "zig-zag" or "break". If there's a proper term for this notation, I haven't found it yet. The closest thing to a "standard" term for this sort of plot appears to be "a broken-axis graph". I call the squiggly part of the axis "the hicky-bob thing".)
My next step is to draw the lines for the median (which is Q2) and the two sub-medians (being the other quartiles, Q1 and Q3), as well as the two extremes:

Then I draw vertical lines to form my box and my whiskers:

I used a graphics program (and its "snap to grid" setting) to make my graphs above nice and neat. For your homework, use a ruler. And it would probably be a good idea to have a six-inch (or fifteen-centimeter) ruler on hand for your next test. Yes, neatness counts.
URL: https://www.purplemath.com/modules/boxwhisk.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()