Return to the Purplemath home page

 
Try a MathHelp.com demo lesson Join MathHelp.com Login to MathHelp.com

 

Index of lessons | Purplemath's lessons in offline form |
Forums | Print this page (print-friendly version) | Find local tutors

 

Venn Diagrams (page 1 of 4)

Sections: Introduction, Logic and set notation, Set-notation exercises, Venn word problems

Venn diagrams were invented by a guy named John Venn (no kidding; that was really his name) as a way of picturing relationships between different groups of things. (Inventing this type of diagram was, apparently, pretty much all he ever accomplished. To add insult to injury, much of what we refer to as "Venn diagrams" are actually "Euler" diagrams. But we'll stick with the usual "Venn" terminology for the purposes of this lesson.) Since the mathematical term for "a group of things" is "a set", Venn diagrams can be used to illustrate both set relationships and logical relationships.

To draw a Venn diagram, you first draw a rectangle which is called your "universe". In the context of Venn diagrams, the universe is not "everything", but "everything you're dealing with right now". Let's deal with the following list of things: moles, swans, rabid skunks, geese, worms, horses, Edmontosorum (a variety of duck-billed dinosaurs), platypusses, and a very fat cat.

  
We'll call our universe "Animals":

 

Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

the 'universe'

  

Let's say we want to classify things according to being small and furry or being a duck-bill. We draw circles to display our classifications:

  
the universe with two circles

  

Now we'll fill in, or "populate", the diagram. Moles, rabid skunks, platypusses, and my (dear departed) cat are all small and furry:

  
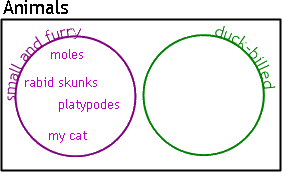
'small and furry' is populated

  

Swans, geese, platypusses, and Edmontosorum are all duck-bills:

  
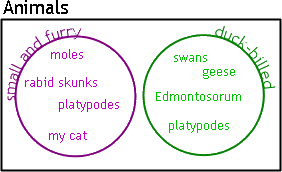
'duck-billed' is populated

  

Worms are small but not furry and horses are furry but not small, and neither is a duck-bill. However, they are animals; they fit inside our universe, but outside the circles.

  
'worms' and 'horses' go outside the circles

  
Notice that "platypusses" is listed in both of the circles. The point of Venn diagrams is that we can show this overlap in set membership by overlapping these circles.

  

In other words, we really should have drawn the circles overlapped, like this:

  
redrawn diagram, with circles overlapping

  

Now when we populate the Venn diagram, we'll only have to write "platypusses" once, in the overlap:

  
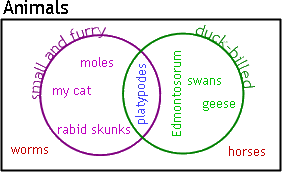
repopulated Venn diagram

The overlap of the two circles, containing only "platypusses", is called the "intersection" of the two sets.

(By the way, the plural of "platypus" is not "platypi", but is, in general [Australian] usage, "platypusses", though I have learned that the technically-correct plural is apparently "platypode".)

When drawing Venn diagrams, you will probably always be dealing with two or three overlapping circles, since having only one circle would be boring, and having four or more circles quickly becomes astonishingly complicated.

Venn diagrams have two general applications: explaining set notation, and doing a certain class of word problems. We'll look at set notation first....

Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Venn Diagrams." Purplemath. Available from
    http://www.purplemath.com/modules/venndiag.htm. Accessed
 

 

 
MATHHELP LESSONS
This lesson may be printed out for your personal use.

Content copyright protected by Copyscape website plagiarism search

  Copyright © 2003-2014  Elizabeth Stapel   |   About   |   Terms of Use   |   Linking   |   Site Licensing

 

 Feedback   |   Error?