Return to the Purplemath home page

 The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra


powered by FreeFind

 

Return to the Lessons Index  | Do the Lessons in Order  |  Get "Purplemath on CD" for offline use  |  Print-friendly page

Venn Diagrams & Set Notation (page 2 of 4)

Sections: Introduction, Logic and set notation, Set-notation exercises, Venn word problems

The following examples should help you understand the notation, terminology, and concepts related to Venn diagrams and set notation.

Let's say that our universe contains the numbers 1, 2, 3, and 4. Let A be the set containing the numbers 1 and 2; that is, A = {1, 2}. (Warning: The curly braces are the customary notation for sets. Do not use parentheses or square brackets.) Let B be the set containing the numbers 2 and 3; that is, B = {2, 3}. Then we have the following relationships, with pinkish shading marking the solution "regions" in the Venn diagrams:

set
notation

pronunciation

meaning

Venn diagram

answer

A U B

"A union B"

everything
that is in
either of the sets

 
A union B is shaded
 

{1, 2, 3}

A ^ B
or
A intersect B

"A intersect B"

only the things
that are in
both of the sets

 
A intersect B is shaded
 

{2}

Ac
or
~A

"A complement",
or "not A"

everything
in the universe
outside of  A

 
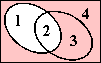
the complement of A is shaded
 

{3, 4}

A – B

"A minus B", or
"A complement B"

everything in A
except for anything
in its overlap with B

 
A complement B is shaded
 

{1}

~(A U  B)

"not (A union B)"

everything
outside
A and B


 the complement of A union B is shaded
 

{4}

~(A ^ B)
or
~(A intersect B)

"not (A intersect B)"

everything outside
of the overlap
of A and B


 the complement of A intersect B is shaded
 

{1, 3, 4}

There are gazillions of other possibilities for set combinations and relationships, but these are among the simplest and most common. Note that different texts use different set notation, so you should not be at all surprised if your text uses still other symbols than those used above. But while the notation may differ, the concepts will be the same. By the way, as you probably noticed, your Venn-diagram "circles" don't have to be perfectly round; ellipses will do just fine.

  • Given the following Venn diagram, shade in A ^ C.

      • three-circle Venn diagramCopyright © Elizabeth Stapel 2003-2011 All Rights Reserved

    The intersection of A and C is just the overlap between those two circles, so:

      the overlap of circles A and C is shaded

  • Given the following Venn diagram, shade in A U(B – C).

      • three-circle Venn diagram

    As usual when faced with parentheses, I'll work from the inside out.

    I'll first find B – C.  "B complement C" means I take B and then throw out its overlap with C, which gives me this:

    B is shaded, except for where it overlaps C

      
    Now I have to union this with     A:

      
    B is shaded except for its overlap with C, and A (including its overlap with C) is fully shaded

Note that unioning with A put some of C (that is, some of what I'd cut out when I did "B – C") back into the answer. This is okay. Just because we threw out C at one point, doesn't mean that it all has to stay out forever.

<< Previous  Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Venn Diagrams & Set Notation." Purplemath. Available from
    http://www.purplemath.com/modules/venndiag2.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  Donating
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

This lesson may be printed out for your personal use.

Content copyright protected by Copyscape website plagiarism search

  Copyright © 2003-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

 Feedback   |   Error?