Trigonometric Functions and Their Graphs: Sine and Cosine

How is the sine ratio also a function?

To convert the sine ratio into a function, we take the unit circle's inputs (being angle measures) and outputs (being sine-ratio values), and extend the process to all angle measures. In other words, we take the 0π-to-2π interval that we're used to using on the unit circle, and expand to all angle measures, including negative ones.

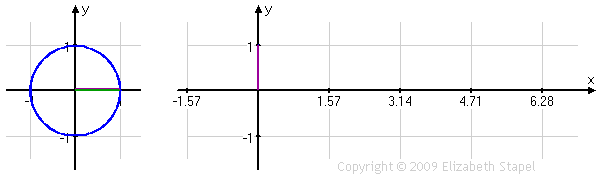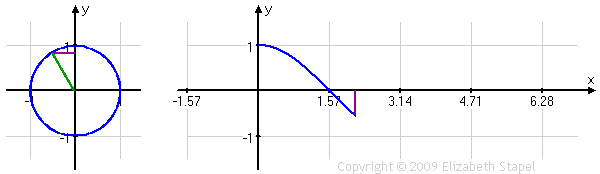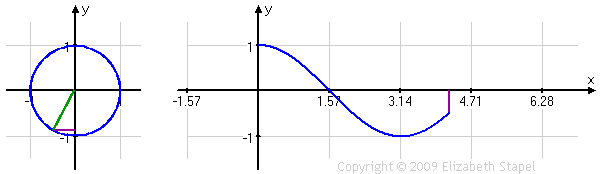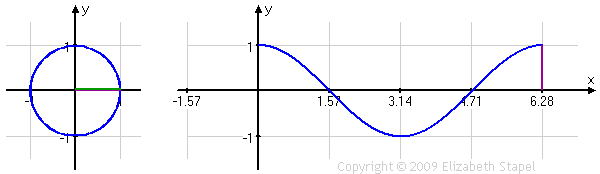
Let's expand a bit on that. Looking at the values of the sine ratio in the four quadrants of the unit circle, we can take the input (that is, the angle measure θ, indicated by the green line in the left-hand graph below), and we can "unwind" those angle values of θ from the unit circle. We can then put those angle values on the horizontal axis of a standard graph in the x,y-plane. Then we can take the output from the unit circle (that is, the values of sin(θ) = y, indicated by the red line in both graphs below), and use these values as the y-value heights above (or depths below) the x-axis, corresponding to the angle-value inputs. The result looks like this:

← swipe to view full image →

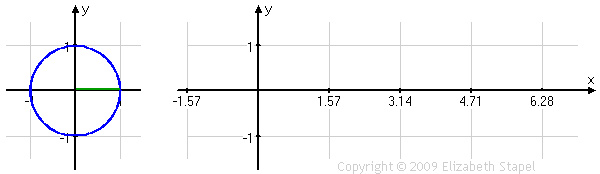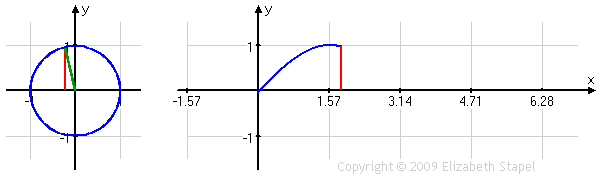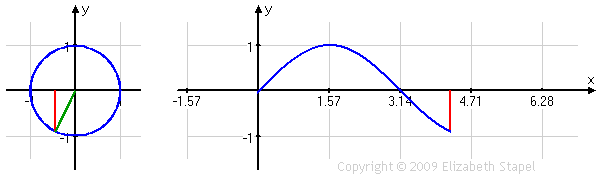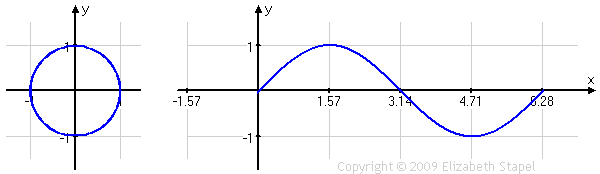
As you can see, the height of the red line, for any given angle-measure input, is the same in each graph. (The green line in the unit circle on the left is contained within the scale of the rectangular (or "regular"-type) graph on the right, which is why the green line is not duplicated on that graph.)

Now let's think a bit more about the unit circle. We typically think of the angles as going from 0π up to (but not quite including) 2π, with the angle-measure resetting each time we re-enter the first quadrant. But we don't have to restrict ourselves to only this interval of angle values; we are allowed to keep counting upward, past 2π, and backwards, before 0π, rather than resetting each rotation.

If the green angle-line in the unit-circle part of the sine-value animation above had gone backwards (that is, in reverse) counting into negative angle measures, the graph on the right would then have extended back to the left of zero. If, instead of starting over again at zero for every revolution on the unit circle, we'd counted up higher angle measuress each time we re-entered the first quadrant in the unit-circle part of the sine-value animation, then the graph on the right would have continued, up and down, over and over again, past 2π and onward to the right.

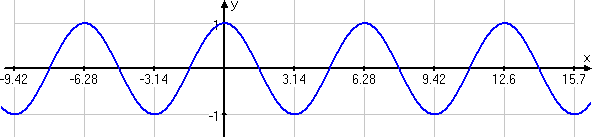
In other words, we would have this graph:

← swipe to view full image →

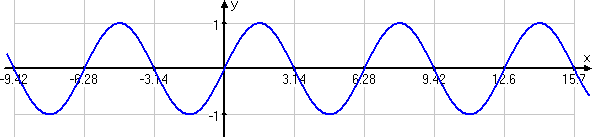
As you can see from the graphic, each input value (each angle measure, which is also an x-value) corresponds with (spits out, results in) a single output value (a sine value, which is also a y-value). Therefore, by unwrapping the sine from the unit circle and rolling it out sideways, we have been able create a function: the sine function, designated as "sin()" (or possibly just [SIN] on your calculator).

The Sine Wave

From the above graph, which shows the sine function from −3π to +5π, you can probably guess why the graph of the sine function is called the sine "wave": the circle's angles repeat themselves with every revolution of the unit circle, so the sine's values repeat themselves with every length of 2π, and the resulting curve is a wave, forever repeating the same up-and-down wave.

(Note: In the graphs above, my horizontal axes are labelled with decimal approximations of π because that's all my equation-grapher software can handle. When you hand-draw graphs, you should instead always use the exact values: π, 2π, π/2, etc.)

---

We can do the same sort of function conversion with the cosine ratio:

← swipe, as needed, to view full image →

The relationship between the cosine's unit circle on the left and its more horizontal graph on the right is a little harder to see here, because the unit circle's output line (the purple line zipping from side to side) is horizontal while the standard graph's output line (also purple, going above and below the x-axis) is vertical. But you can see how those two purple lines have the same length at the same angle values (that is, at the same point within the period), as those values move from zero to 2π.

The Cosine Wave

Just as with the sine graph, the cosine graph can be extended outside the interval from zero to 2π, infinitely in each horizontal direction:

← swipe, as needed, to view full image →

Just as with the sine graph, the cosine graph above repeats itself as a wave, up and down, forever. And just as with the sine ratio that we converted into a function, we have now been able to extend the cosine ratio into a cosine function, designated "cos()" (or just [COS] on your calculator).

What is periodicity for sine and cosine?

As you can see from the extended sine and cosine graphs, these curves repeat themselves every time they pass a multiple of 2π. This trait is called "periodicity", because the graph has a "period" (that is, a fixed-length interval) over which the curve repeats itself. The length of the period for the sine and cosine curves is clearly 2π. This makes sense, since they are each derived from going "once around" a circle.

For sines and cosines, their periodicity means that their original pattern, falling between 0π and 2π, will restart at 2π and will repeat the original pattern between 2π and 4π; they will again restart and repeat between 4π and 6π; they will also restart and repeat between −4π and −2π; and so forth.

(This can be helpful for graphing. If an exercise specifies that you must show the graph "over two periods" or some other non-original-period interval, you can do the original-period graph, and then just duplicate everything in the additional periods.)

What is amplitude for sine and cosine?

The sine and cosine functions each vary in height, as their waves go up and down, between the y-values of −1 and +1. This value of "1" is called the "amplitude" of the waves.

Note that the sine and cosine curves go one unit above and below their midlines; here, the midline happens to be the x-axis. But sines and cosines can be translated up or down by adding or subtracting some number to the function. But even the pushed-up or pulled-down sines and cosines will still wave up and down a fixed distance above and below their midlines. So even if you were given the function f(x) = sin(x) + 4, so the wave was centered four units above the x axis, the wave would go no higher than 5 and no lower than 3; their amplitudes would still be 1.

If the sine or cosine function is transformed by multiplication, then this will change the amplitude. For instance, if you were given g(x) = 3cos(x), the multiplier "3" will multiply all of the cosine's values, so that the curve will vary between −3 and +3. In this case, the amplitude of the function would be 3. (The amplitude would also be 3 for the function h(x) = −3cos(x); the only difference would be that this wave would be upside-down from the regular cosine wave.)

How can I easily graph sines and cosines?

When you graph, it isn't necessary to plot loads of points. You might want to when you're a beginner, but you will quickly notice that some points of these waves are more useful (interesting, regular) than nearly all of the others.

For instance, at either end of the standard period (that is, where x = 0 and x = 2π), the cosine wave is at height y = 1. Draw those two dots. In the middle of the period, for x = π, the cosine wave is at y = −1. Draw that dot. The midpoints of each half of the standard period are at x = π/2 and x = 3π/2; at these points, the cosine wave is at y = 0 (that is, it's on or crossing the x-axis). Draw these two dots.

Plot these five "interesting" points, and then fill in the curve.

Correspondingly, when you do your sine graphs, use the five useful points. At either end of the standard period (that is, where x = 0 and x = 2π), the sine wave is at y = 0 (that is, it's on or crossing the x-axis). Draw those two dots. In the middle of the period, for x = π, the sine wave is again crossing the x-axis. Draw that dot. At the midpoint of the first half of the period (that is, at x = π/2), the height of the sine wave is y = 1; draw that dot. At the midpoint of the second half of the period (that is, at x = 3π/2), the height of the sine wave is y = −1; draw that dot.

(For info on how to graph transformed sines and cosines, please see "Graphing Trigonometric Functions".)