Completing the Square: Finding the Vertex (page 1 of 2)

The vertex form of a quadratic is given by
y = a(x – h)² + k, where (h, k) is the vertex.
The "a" in the vertex form is the same "a" as
in y = ax² + bx + c (that is, both a's have exactly the same value). The sign on "a" tells you whether the quadratic opens up or opens down. Think of it this way: A positive "a" draws a smiley, and a negative "a" draws a frowny. (Yes, it's a silly picture to have in your head, but it makes is very easy to remember how the leading coefficient works.)

In the vertex form of the quadratic, the fact that (h, k) is the vertex makes sense if you think about it for a minute, and it's because the quantity "x – h" is squared, so its value is always zero or greater; being squared, it can never be negative.

Suppose that "a" is positive, so a(x – h)² is zero or positive and, whatever x-value you choose, you're always taking k and adding a(x – h)² to it. That is, the smallest value y can be is just k; otherwise y will equal k plus something positive. When does y equal only k? When x – h, the squared part, is zero; in other words, when x = h. So the lowest value that y can have, y = k, will only happen if x = h. And the lowest point on a positive quadratic is of course the vertex.

If, on the other hand, you suppose that "a" is negative, the exact same reasoning holds, except that you're always taking k and subtracting the squared part from it, so the highest value y can achieve is y = k at x = h. And the highest point on a negative quadratic is of course the vertex.

They don't usually give you the quadratic in vertex form; instead, they usually give you the quadratic in the regular y = ax² + bx + c format. How do you convert from the regular format to the vertex format? By using the technique of completing the square. Here's an example:

• Find the vertex of y = 3x² + 2x – 1

Follow this procedure: Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved

This is your original equation.	y = 3x2 + 2x – 1
Move the loose number over to the other side.	y + 1 = 3x2 + 2x
Factor out whatever is multiplied on the squared term. Remember that "factor" does not mean to "make disappear" or "divide off onto the other side"; "factor" means "divide out front".
Create space on the left-hand side, and, if "a" is anything other than 1, put a copy of "a" in front of this space. You'll need this space and the copy of "a" to keep your equation "balanced". Take half of the coefficient of the x-term from inside the right-hand side parentheses (that is, divide it by two, not forgetting its sign). Square the result, and add it to both sides inside the parentheses.
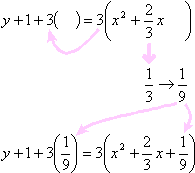
Multiply out the "a times the squared coefficient" part on the left-hand side, and convert the right-hand side to squared form. (This is where you use that sign you kept track of earlier, putting that sign in the middle of the squared expression.)
Simplify some more, as necessary.
Move the loose number back over to the right-hand side.
To be thorough, reformat into vertex form, and read off the vaues of "h" and "k".

In this case, since a = 3, and three is positive, then this is a right-side-up parabola, and the vertex, (h, k) = ( ^–1/₃ , ^–4/₃ ), is the lowest point on the graph.

Why did I reformat things in that last line? Because the formula for the vertex form is y = a(x – h)² + k. In other words, I needed to make clear the value that was subtracted to get "x + ¹/₃"? To get a "plus" in the simplified form, I had to have subtracted a negative:

x – ( ^–1/₃ ) = x +  ¹/₃

The negatives cancelled to give me the "plus". And what was added to get " ^{– 4} / ₃"? I had to have added a negative number, ^{– 4} / ₃, because + ( ^{– 4} / ₃ ) = ^{– 4} / ₃.

Warning: It's easy to confuse yourself at that final stage, by trying to read off the vertex as " (h, k) = (whatever number is inside the squared part, whatever the other number is) ", without noticing the fact that the h-part is subtracted and the k-part is added. If you take care to ensure that you have your quadratic completely converted to vertex form by being careful of the signs, then you'll be able to avoid one of the most commonly-made mistakes for these problems. Make sure you practice this until you can consistently interpret your results correctly.

By the way, did you notice that the vertex coordinates weren't whole numbers? Instructors are starting to figure out that students are guessing the vertex from the pretty pictures in their graphing calculators, and they know that students often have the idea that all answers are always either whole numbers or "neat" fractions. For instance, if the calculator screen estimates a vertex as being at (0.48, 0.98), many students will assume that the answer must "really" be (0.5, 1), instead of, say, ( ¹²/₂₅, ⁴⁹/₅₀ ).

So, in order to check that students really do know how to find the vertex (and not just guess a decimal approximation from a picture), teachers are giving more complicated exercises. If you have been told that you should know this technique for finding the vertex, rest assured that your teacher has ways of checking whether you have really learned this. Don't plan on using calculator cheats.

Top  |  1 | 2  |  Return to Index  Next >>

  Copyright © 2000-2014  Elizabeth Stapel   |   About   |   Terms of Use   |   Linking   |   Site Licensing

 Feedback   |   Error?