The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Completing the Square: Quadratic Examples
     & Deriving the Quadratic Formula (page 2 of 2)

• Solve x² + 6x + 10 = 0.

Apply the same procedure as on the previous page:

This is the original equation.	x2 + 6x + 10 = 0
Move the loose number over to the other side.	x2 + 6x = – 10
Take half of the coefficient on the x-term (that is, divide it by two, and keeping the sign), and square it. Add this squares value to both sides of the equation.
Convert the left-hand side to squared form.  Simplify the right-hand side. Note: If you don't know about complex numbers yet, then you have to stop at this step, because a square can't equal a negative number! Otherwise, proceed...	(x + 3)2 = –1 Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved
Square-root both sides. Remember to put the "±" on the right-hand side.
Solve for "x =", and simplify as necessary.	x = –3 ± i

If you don't yet know about complex numbers (the numbers with "i" in them), then you would say that the above quadratic has "no solution". If you do know about complexes, then you would say that this quadratic has "no real solution" or that is has a "complex solution".

Since solving "(quadratic) = 0" for x is the same as finding the x-intercepts (assuming the solutions are real numbers), it stands to reason that this quadratic should not intersect the x-axis (since x-intercepts are "real" numbers). As you can see below, the graph does not in fact cross the x-axis.

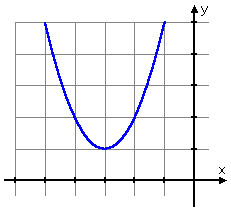
This relationship is always true. If you come up with a real value on the right-hand side of the equation (a zero value is real, by the way; the square root of zero is just zero), then the quadratic will have two x-intercepts (or only one, if you get plus/minus of zero on the right side); if you get a negative on the right-hand side, then the quadratic will not cross the x-axis.

I'll do one last "example". It has become somewhat fashionable to have students derive the Quadratic Formula themselves; this is done by completing the square for the generic quadratic equation ax² + bx + c = 0. While I can understand the impulse (showing students how the Formula was invented, and thereby giving an example of the usefulness of symbolic manipulation), the computations involved are often a bit beyond the average student at this point. Here is what the instructor is looking for:

• Derive the Quadratic Formula by solving ax² + bx + c = 0.
    

This is the original equation.	ax2 + bx + c = 0
Move the loose number to the other side.	ax2 + bx = –c
Divide through by whatever is multiplied on the squared term. Take half of the x-term, and square it. Add the squared term to both sides.
Simplify on the right-hand side; in this case, simplify by converting to a common denominator.
Convert the left-hand side to square form (and do a bit more simplifying on the right).
Square-root both sides, remembering to put the "±" on the right.
Solve for "x =", and simplify as necessary.

Whether you're working symbolically (as in the last example) or numerically (which is the norm), the key to solving by completing the square is to practice, practice, practice. By so doing, the process will become a bit more "automatic", and you'll remember the steps when you're taking the test.

<< Previous  Top  |  1 | 2  |  Return to Index

  Copyright © 1999-2010  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?