"The Relationship" for Logarithms
Purplemath
What are logarithms?
Logarithms are the opposite of exponentials, just as subtraction is the opposite of addition and division is the opposite of multiplication. Logs undo exponentials.
Technically speaking, log functions are the inverses of exponential functions.
Content Continues Below
Why are logs so hard?
I think logarithms, both as mathematical things and also as a concept, are difficult because they consist of so many concepts piled onto each other all at once, and because there is a fair amount of backwardness to them. Logarithms are inverse functions (backwards), and logs represent exponents (concept), and taking logs is the undoing of exponentials (backwards and a concept). And this is a lot to take in all at once.
Affiliate
Advertisement
Yes, in a sense, logarithms are themselves exponents. Logarithms have bases, just as do exponentials; for instance, log5(25) stands for the power that you have to put on the base 5 in order to get the argument 25. So log5(25) = 2, because 52 = 25.
But, in all fairness, I have yet to meet a student who understands this explanation the first time they hear it. It took me the better part of a week of diligent study to finally understand logs at all. Then, oddly, I woke up one morning and realized, while watching myself in the mirror as I brushed my teeth, that I *totally* "got" them. Logs finally made perfect sense.
When helping other students with logs (tutoring, grading homework, working in the Math Help room, etc), I saw that this seemed to be everybody's experience. Nobody "gets" it from the math-ese explanations in textbooks and classrooms. The best I could do was to repeat the "logs are exponents" concept until it finally somehow sank in. It was always a painful process. So, for years, I searched for a better way to explain them.
Then it dawned on me: The lengthy conceptual explanation, with all of its inverse-function working-backward-ness, was, well, too long. Wouldn't it be nice if there were a short version, or maybe just a name?
So I made up a name, and it worked. Students were able to understand logs on the first day. Yay!
What is the easy way to understand logarithms?
An easier way to understand logarithms is to give a name to its fundamental definition of being the inverse function of exponentials; I've named this "The Relationship", which is:
— The Relationship —
y = bx
is equivalent to
(that is, it means the exact same thing as)
logb(y) = x
On the first line below the title above is the exponential statement:
y = bx
On the last line above is the equivalent logarithmic statement:
logb(y) = x
The log statement is pronounced as "log-base-b of y equals x". The value of the subscripted base b is "the base of the logarithm", just as b is the base in the exponential expression bx.
And, just as the base b in an exponential is always positive and not equal to 1, so also the base b for a logarithm is always positive and not equal to 1.
Whatever is inside the logarithm is called the argument of the log.
Note that the base in both the exponential equation and the log equation is b, but that the x and y switch sides when you switch between the two equations. This correspondence is highlighted in The Relationship, animated below:
— The Relationship, Animated —
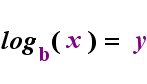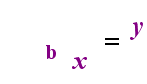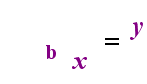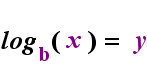
(The above graphic is animated on the live webpage.)
The Relationship says that whatever had been the argument of the log becomes the "equals" on the other side of the equation, and whatever had been the "equals" becomes the exponent in the exponential, and vice versa.
Affiliate
If you can keep this straight in your head, then you shouldn't have too much trouble with logarithms.
(I coined the term "The Relationship" myself. You will not find it in your text, and your teachers and tutors will likely have no idea what you're talking about if you mention it to them. "The Relationship" is entirely non-standard terminology. Why do I use it anyway? Because it works.)
By the way: If you noticed that I switched the variables between the two boxes displaying The Relationship, you've got a sharp eye. I did that on purpose, to stress that the point of The Relationship is not the variables themselves, but how they move.
Content Continues Below
How are logarithms useful?
Originally, logarithms were invented as a way of converting multiplication into addition. (Using logs was an improvement over using trigonometric identities.) When people were needing to multiply big numbers (or numbers with plenty of decimal places), they would take the numbers in the multiplication (let's call them a and b) and take the base-10 log of the product. This allowed them to convert the product into a sum by using a rule for logs:
log(ab) = log(a) + log(b)
Then they would refer to a table of log values, and find the inputs that most-closely matched the first few digits of each of a and b. They would copy down those values, and replace the added logs with these output values (let's call them c and d). The addition was easy; let's call the summed value s. They would then return to the log tables, using them this time to work backwards.
If we name the value of 10s as t, the then process would look something like this:
a × b
log(a × b)
log(a) + log(b)
c + d
c + d = s
10s = t
By this process, the person doing the calculations would be able to say that ab was equal to t, at least for the first few digits.
Remember, this was waaaaay before electronic calculators were invented. Suppose you were a scientist in, say, the 1700's, and you needed to multiply some really big numbers. You could spend a good while doing it yourself, you could hire an autistic savant (a real-life "Rain Man" such as Thomas Fuller or Jedediah Buxton) to do the math for you (in a matter of seconds), or you could resort to log tables.
Most scientists didn't have a savant in their employ. So, when logarithms were invented, they were adopted by mathematicians and scientists as major time-savers. Eventually, slide-rules were invented as a means of making log-based computations even easier and quicker.
"But", I hear you cry; "we have calculators and computers now; why do we still use logs?" We still use logs because they can, in a sense, tame exponential growth.
Exponential growth is fast. Values get bigger and bigger, faster and faster, the larger the value of the exponent. This makes for a graph that shoots up and out of the top of your graph, and can make computations unweildy (or, for us puny humans, can make relationships difficult to comprehend). When graphing or when working with relationships between two data sets, straight lines are the Holy Grail. Straight lines are simpler than curvy ones. And smaller numbers fit our brains better.
So, when dealing with exponential growth, we can take the logs of the big numbers, and reduce them down to values that we can better comprehend. For instance, the earthquake scale is logarithmic. An earthquake of magnitude 5 is ten times the strength of an earthquake of magnitude 4, and the numbers 4 and 5 are easier for us to track than are, say, 10,000 and 100,000.
In just about any physical situation in which you have exponential growth, logarithms can be helpful. Straight lines are nice.
Probably the first thing you'll be asked to do with logarithms is to convert back and forth between logs and exponentials.
- Convert 63 = 216 to the equivalent logarithmic expression.
The Relationship tells me that, to convert this exponential statement to logarithmic form, I should leave the base (that is, the 6) where it is, but lower it to make it the base of the log; and I should have the 3 and the 216 switch sides, with the 3 being the value of the log6(216). This gives me:
log6(216) = 3
- Convert log4(1024) = 5 to the equivalent exponential expression.
The Relationship tells me that, to convert this log expression to exponential form, I need to keep the base (that is, the 4) on the left-hand side; and I should have the 1024 and the 5 switch sides, with the5 being the power on the 4. This gives me:
45 = 1024
- Convert ax = d to the equivalent logarithmic form.
In the exponential equation that they've given me, there are no numerical values; everything is symbolic algebra. But that's okay; The Relationship works just fine with this.
To convert the exponential form to logarithmic form, I need to make the base b the base of the logarithm, and switch sides with the x and the d. So my answer is:
logb(d) = x
- Convert logp(q) = r to the equivalent exponential form.
There are no numbers in the logarithmic equation, but that's okay. I'll apply The Relationship, keeping the base of p and swapping sides with the q and the r. Then my answer is:
pr = q
URL: https://www.purplemath.com/modules/logs.htm
You can use the Mathway widget below to practice converting logarithmic statements into their equivalent exponential statements. Try the entered exercise, or type in your own exercise. Then click the button (and, if necessary, select "Write in Exponential form") to compare your answer to Mathway's. (Or skip the widget, and continue to the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()