3-by-3 Determinants

Create the determinant by replacing the square brackets with absolute-value bars:

The above is the determinant of the 3-by-3 matrix. But to find the value of that determinant (that is, when you're doing your actual computations), remove those bars and extend the determinant's grid by rewriting the first two columns of numbers after (that is, to the right of) the third column in the grid of numbers. You should get the following array:

When we were finding determinants of 2-by-2 matrices, we multiplied diagonally and then subtracted the "up and to the right" value from the "down and to the right" value. With the extended grid of numbers that we've created here, we can do something similar.

Starting from the top left corner, we multiply along the (first three) down-diagonals:

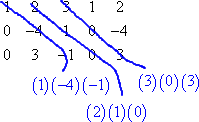
Then, starting from the bottom left corner, we multiply along the (first three) up-diagonals:

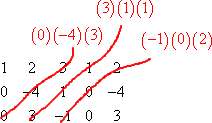
Add the down-diagonals and subtract the up-diagonals:

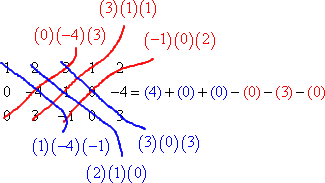
Note my use of parentheses above. This can help keep track of signs, especially if you're needing to subtract a negative number.

Now that I've done my multiplying, and have set up my additions and subtractions, it's time to simplify:

Then my hand-in answer is:

First I convert from the matrix to the set-up for finding its determinant by removing the square brackets, and adding the first two columns to the right of the grid of numbers:

Then I multiply down and up the six diagonals:

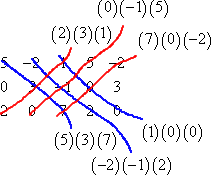
Finally, I add the down-diagonals, subtract the up-diagonals, and simplify for the final answer:

Then my hand-in answer is: