An Explanation of Minors and Cofactors
Purplemath
Finding the determinant of a 2×2 matrix is easy: You just do the criss-cross multiplication, and subtract:

Content Continues Below
The process for finding the determinants of 3×3 matrices, while a bit messier, is still pretty straightforward: You add repeats of the first and second columns to the end of the determinant, multiply along all the diagonals, and add and subtract according to the rule:
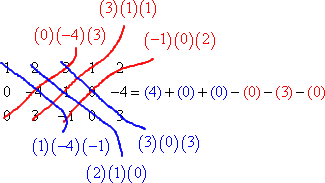
But for 4×4's and bigger determinants, you have to drop back down to the smaller 2×2 and 3×3 determinants by using things called "minors" and "cofactors".
What is a minor of a matrix's determinant?
A minor of a determinant is the determinant formed by deleting one row and one column from the original determinant. And, since there are lots of rows and columns in the original determinant, you can make lots of minors from it.
Affiliate
Advertisement
How are individual minors labelled or named?
Minors are labelled according to the row and column that were deleted from the original determinant. So if you were to go, say, to the a2,4 entry from the determinant of some matrix A and cross out the row and column that pass through that entry (that is, if you remove the second row and the fourth column from the determinant), the new (and smaller) determinant is called the minor M2,4.
The following is an example of this:
the determinant A:
cross out all entries sharing a row or column with entry a2,4:
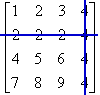
the minor M2,4:
Once you find a minor Mi, j, it's time to find the cofactor.
What is a cofactor of a matrix's determinant?
A cofactor corresponds to the minor for a certain entry of the matrix's determinant. To find the cofactor of a certain entry in that determinant, follow these steps:
- Take the values of i and j from the subscript of the minor, Mi,j, and add them.
- Take the value of i + j and put it, as a power, on −1; in other words, evaluate (−1)i+j.
- Multiply the minor Mi,j by the result in Step 2.
The result of (−1)i+jMi,j is the cofactor, Ci,j.
You're still not done though. Yes, there's more.
Content Continues Below
How do you find the determinant using minors and cofactors?
To find the determinant of the matrix A by using minors and cofactors, you have to pick a row or a column of the matrix, find all the cofactors for that row or column, multiply each cofactor by its corresponding matrix entry, and then add all the values you've gotten.
Okay, yeah; that probably didn't make much sense. Here's another way of saying it:
- You've got some matrix A. You need to find the determinant of it.
- The matrix is too big to find its determinant by the simpler methods, so you'll have to find it by "expanding along a row or column".
Affiliate
How do you expand along a row or column?
To find the value of a determinant of a larger matrix by using minors and cofactors, you will need to "expand along a row or column" by the following steps:
- Picking a row or a column along which you will do the expansion. Let's say you pick the third row.
- For each entry in the third row, you will find the cofactor of that entry and multiply the entry by its cofactor. That is, for the a3,1 entry of the matrix A, you will find the cofactor C3,1, and then you'll multiply the cofactor by the a3,1 entry: (a3,1)(C3,1). For entry a3,2, you will find the cofactor C3,2, and multiply: (a3,2)(A3,2). And so forth.
- Then you will add up all of these products: (a3,1)(C3,1) + (a3,2)(C3,2) + (a3,3)(C3,3) + ....
The resulting sum is the value of the determinant of the matrix A.
(The above convoluted messiness is why nobody does determinants by hand if it can be avoided: there's just so much error-prone mindless grunt-work involved.)
It doesn't matter which row or column you use for your expansion; you'll get the same value regardless. But this flexibility can be useful, because it can let you aim at zeroes.
- Find the determinant of the following matrix by expanding (a) along the first row and (b) along the third column. (c) Compare the results of each expansion.
(a) To expand along the first row, I need to find the minors and then the cofactors of the first-row entries; that is, I need to find the minors for the matrix entries a1,1, a1,2, a1,3, and a1,4, and then multiply them by −1 or +1 to get the cofactors.
M1,1:
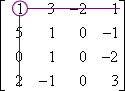
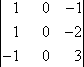
M1,1 = 0
C1,1 = (−1)1+1 × 0 = 0
M1,2:
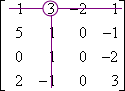
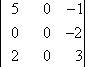
M1,2 = 0
C1,2 = (−1)1+2 × 0 = 0
M1,3:
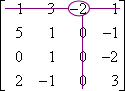
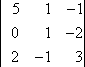
M1,3 = 3
C1,3 = (−1)1+3 × 3 = 3
M1,4:
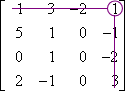
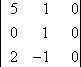
M1,4 = 3
C1,4 = (−1)1+4 × 0 = 0
So the determinant of this matrix, found by expanding along the first row, is:
(a) det(A) = a1,1C1,1 + a1,2C1,2 + a1,3C1,3 + a1,4C1,4
= 1(0) + 3(0) + (−2)(3) + 1(0) = −6
(b) To expand along the third column, I need to find the minors and then the cofactors of the third-column entries: a1,3, a2,3, a3,3, and a4,3.
M3,1:
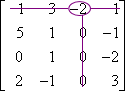
M3,1 = 3
C3,1 = (−1)3+1 × 3 = 3
Wait a sec... The a2,3-entry of the original matrix is zero. This means that I'll be getting zero for that term when I expand down the column, no matter what the value of the minor M2,3 turns out to be. So I don't really care what the C2,3 cofactor is; I can just put 0 for this entry, because:
a2,3C2,3 = (0)(C2,3) = 0
In fact, I can ignore *each* of the last three terms in the expansion down the third column, because the third column's entries (other than the first entry that I've already done) are all going to equal zero.
So the only computation I care about is one I've already done:
(b) det(A) = a1,3C1,3
= (−2)(3) = −6
For part (c) of this exercise, I'm supposed to compare the two determinant values.
(c) Comparison: Each expansion gives the same value.
The point of this exercise is to show that it doesn't matter across which row or down which column you do your expansion; the value you get (assuming no arithmetic errors) will always be the same. This means that you can pick the row or column that you view as being the easiest, and it won't affect your final answer.
URL: https://www.purplemath.com/modules/minors.htm
You can use the Mathway widget below to practice finding cofactors. Try the entered exercise, or type in your own exercise. (Or skip the widget and go to the next page.) Then click the button and select "Find the Cofactor Matrix", which shows *all* the cofactors, to compare your answer to Mathway's. (You may first have to click "More..." to see the cofactor-matrix option. The cofactor matrix shows the cofactors for every entry in the original matrix.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




