The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Right-Triangle Word Problems

Once you've learned about trigonometric ratios (and their inverses), you can solve triangles. Naturally, many of these triangles will be presented in the context of word problems. A good first step, after reading the entire exercise, is to draw a right triangle and try to figure out how to label it. Once you've got a helpful diagram, the math is usually pretty straightforward.

• A six-meter-long ladder leans against a building. If the ladder makes an angle of 60° with the ground, how far up the wall does the ladder reach? How far from the wall is the base of the ladder? Round your answers to two decimal places, as needed.
   

First, I'll draw a picture. It doesn't have to be "good"; it just needs to be clear enough that I can keep track of what I'm doing. My picture is at right: I need to find the height h. Since they've given me an angle measure and "opposite" and the hypotenuse for this angle, I'll use the sine ratio for finding the height: sin(60°) = h/6 6×sin(60°) = h = 3sqrt[3] Plugging this into my calculator, I get an approximate value of 5.196152423.

For the base, I'll use the cosine ratio:

cos(60°) = b/6
6×cos(60°) = b = 3

The ladder reaches about 5.20 meters up the wall,
and its base is 3 meters from the wall.

Note: Unless you are told to give your answer in decimal form, or to round, or in some other way not to give an "exact" answer, you should probably assume that the "exact" form is what they're wanting. For instance, if they hadn't told me to round in the exercise above, my value for the height should have been the value with the radical.

• A five-meter-long ladder leans against a wall, with the top of the ladder being four meters above the ground. What is the approximate angle that the ladder makes with the ground?
   

As usual, I'll start with a picture:

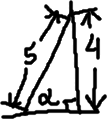
They've given me the "opposite" and the hypotenuse, and asked me for the angle value. For this, I'll need to use inverse trig ratios.

sin(α) = 4/5
α = sin^–1(4/5) = 53.13010235...

The angle the ladder makes with the ground is about 53°.

• You use a transit to measure the angle of the sun in the sky; the sun fills 34' of arc. Assuming the sun is 92,919,800 miles away, find the diameter of the sun. Round your answer to the nearest mile.

First, I'll draw a picture:   Hmm... This "ice-cream cone" picture doesn't give me much to work with, and there's no right triangle.   The two lines along the side of my triangle measure the lines of sight from Earth to the sides of the Sun. What if I add another line, being the direct line from Earth to the center of the Sun?   Now that I've got this added line, I have a right triangle; two right triangles, actually, but I only need one. Because the Sun is so far away, obviously this picture is not "to scale", and I'll have to ignore the fact that the distance measured doesn't quite match the picture. But this should be good enough. (The angle measure, "thirty-four arc minutes", is equal to 34/60 degrees. Dividing this in half is how I got 17/60 of a degree for the smaller angle.)

I need to find the width of the Sun. That width will be twice the base of one of the right triangles. With respect to my angle, they've given me the "adjacent" and have asked for the "opposite", so I'll use the tangent ratio:

tan(17/60°) = b/92919800
92919800×tan(17/60°) = b = 459501.4065...

This is just half the width; carrying the calculations in my calculator (to minimize round-off error), I get a value of 919002.8129. This is higher than the actual diameter, which is closer to 864,900 miles, but this value will suffice for the purposes of this exercise.

The diameter is about 919,003 miles.

• A private plane flies 1.3 hours at 110 mph on a bearing of 40°. Then it turns and continues another 1.5 hours at the same speed, but on a bearing of 130°. At the end of this time, how far is the plane from its starting point? What is its bearing from that starting point?

The bearings tell me the angles from "due north", in a clockwise direction. Since 130 – 40 = 90, these two bearings will give me a right triangle. From the times and rates, I can find the distances: Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved

1.3 × 110 = 143
1.5 × 110 = 165

Now that I have the lengths of the two legs, I can set up a triangle:

I can find the distance by using the Pythagorean Theorem:

143² + 165² = c²
20449 + 27225 = c²
47674 = c²
c = 218.3437657...

The 165 is opposite the unknown angle, and the 143 is adjacent, so I'll use the inverse of the tangent ratio to find the angle's measure:

165/143 = tan(θ)
tan^–1(165/143) = θ = 49.08561678...

But this is not the "bearing", since the bearing is the angle with respect to "due north". I need to add in the original forty-degree angle to get my answer:

The plane is about 218 miles away, at a bearing of about 89°.

Another major class of right-triangle word problems you will likely encounter is angles of elevation and depression....

Top  |  Return to Index

  Copyright © 2010-2012  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?