Multiplicities & "Flexing"
Purplemath
There's an extra detail I'd like to mention regarding the multiplicity of a zero and the graph of the polynomial. That detail is the fact that you can tell, from the graph, whether an odd-multiplicity zero occurs only once, or if it occurs more than once.
You can see the difference in how the graph crosses the x-axis. If it crosses in the manner that you're used to, from graphing straight lines, then the zero is of multiplicity one. If, on the other hand, the graph "flexes" or "flattens out" to some degree when it goes to cross the axis, then the zero is of a higher multiplicity; that is, it'll be of multiplicity three, five, or higher.
Here's an example of how this works:
Content Continues Below
-
What is the multiplicity of x = 5, given that the graph shows a fifth-degree polynomial with all real-number roots, and the root x = −5 has a multiplicity of 2?
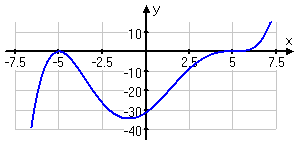
The intercept at x = −5 is clearly of even degree, because the graph just "kisses" the axis there, and then turns back the way it came. So this zero could be of multiplicity two, or four, or six, etc. But they've specified for me that the intercept at x = −5 is of multiplicity 2.
The polynomial is of degree 5, and there are no non-real zeroes. The zero at x = 5, the only other zero, is clearly of odd degree (so of degree one or three) and, because there are no non-real zeroes, this second root must use up the rest of the multiplicities. Since 5 − 2 = 3, then:
x = 5 is of multiplicity 3.
Affiliate
Advertisement
The zero at x = 5 had to be of odd multiplicity, since the graph went through the x-axis. But the graph flexed a bit (the "flexing" being that bendy part of the graph, where the curve flattened its upward course) right in the area of x = 5. This flexing and flattening is what tells us that the multiplicity of x = 5 has to be more than just 1.
In this particular case, the multiplicity couldn't have been 5 or 7 or more, because the degree of the whole polynomial was only 5. But the multiplicity certainly had to be more than just 1.
Keep this in mind: Any odd-multiplicity zero that flexes at the crossing point, like this graph did at x = 5, is of odd multiplicity 3 or more.
Note: If you get that odd flexing behavior at some location on the graph that is off the x-axis (above or below the axis), then you're probably looking at the effect of complex zeroes; namely, the zeroes that you'd find by using the Quadratic Formula or some other complication; in other words, they're the zeroes that don't correspond to the graph crossing the x-axis.
-
Which of the following graphs could represent the polynomial f (x) = a(x − b)2(x − c)3?
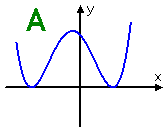
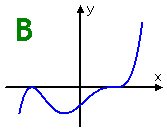

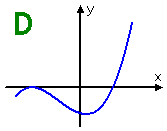
They've given me roots b and c, but they haven't given me numerical values for b and c. But that's okay. I don't need to know the actual values; all I need is the multiplicities. From the behavior for various multiplicities, I'll be able to figure out which is the correct graph.
Affiliate
I can find the degree of the polynomial by adding the powers of its factors. So, whatever this polynomial might be, I can be certain that it is of degree 5. Why? Because, if I bothered to multiply everything out, the degree on the leading term would be 5.
The degree here then is odd. Since the polynomial is of odd degree, then Graph A can't be correct, because its ends both go the same direction, meaning it is an even-degree polynomial. This leaves me with Graphs B, C, and D.
Since my polynomial has two real-number zeroes (namely, zeroes at x = b and at x = c), I know that Graph C can't be right, because it only crosses the x-axis once. So Graph C is correctly of odd degree, but it doesn't have the right number of real zeroes. This leaves me with Graphs B and D.
From the end behavior, I can see that Graph D is of odd degree. Also, I know that the negative zero has an even multiplicity because the graph just touches the axis; this zero could correspond to x = b. But there is no flexing where the graph crosses the positive x-axis, so the odd zero here must have a multiplicity of only 1, and I need the multiplicity of this zero to be more than just 1; I need it to be of multiplicity 3. So Graph D may have the correct degree (if the zero x = b is of multiplicity 1), but the multiplicities of the two zeroes don't match up with what I need. This leaves me with Graph B (or else "none of the above").
Looking at the remaining graph, I see that the ends of the graph tell me that Graph B is of odd degree (because one end is down and the other end is up), and the way the graph touches or crosses the x-axis at the two graphed x-intercepts tells me that the polynomial being graphed has one even-multiplicity zero and one odd-and-more-than-1 multiplicity zero. This matches what I need. So:
The correct graph is Graph B.
Content Continues Below
-
Find the degree-7 polynomial corresponding to the following graph, given that one of the zeroes has multiplicity 3.
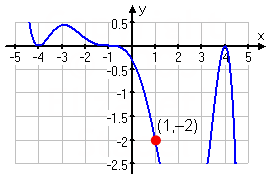
They want me to figure out exact values from a picture, so I'm safe here in assuming that values that look like they're integer values really are integer values. (This of course isn't the case "in real life". But they have to give me nice neat numbers if they're having me guess from the drawing.
From the graph, I can see that there are zeroes of even multiplicity at x = −4 and x = 4. How do I know this? Because the graph just touches the x-axis at these x-values, and then turns back the way it came. So these two zeroes give me at least four of the total seven degrees for this polynomial.
The one remaining root, the zero at x = −1, must be the zero of multiplicity 3. This matches the graph, since the line goes through the axis, but flexes as it does so, telling me that the multiplicity must be odd and must be more than 1.
Since the total degree of the polynomial is 7, and I already have multiplicities of 2, 2, and 3 (which adds up to 7), then the zeroes at −4 and 4 must be of multiplicity 2, rather than multiplicity 4 or multiplicity 6 or something bigger.
Working backwards from the zeroes, I get the following expression for the polynomial:
y = a(x + 4)2(x + 1)3(x − 4)2
They marked that one point on the graph so that I can figure out the exact polynomial; that is, so I can figure out the value of the leading coefficient "a". Plugging in these x- and y-values from the point (1, −2), I get:
a(1 + 4)2(1 + 1)3(1 − 4)2
= a(25)(8)(9)
= 1800a = −2
Solving the last line above for the value of the one remaining variable, I get that . Then the polynomial, in factored form, is:
Affiliate
The exercise didn't say that I had to multiply this out, so I'm not going to. The factored form (especially for something as huge as this) should be a completely acceptable form of the answer.
URL: https://www.purplemath.com/modules/polyends3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



