Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Scalar and Matrix Multiplication (page 1 of 3)

There are two types of multiplication for matrices: scalar multiplication and matrix multiplication. Scalar multiplication is easy. You just take a regular number (called a "scalar") and multiply it on every entry in the matrix.

  • For the following matrix A, find 2A and –1A.

      • A = [[ 1 2 ][ 3 4 ]]

    To do the first scalar multiplication to find 2A, I just multiply a 2 on every entry in the matrix:

      2A = 2 × [[ 1 2 ][ 3 4 ]] = [[ 2×1 2×2 ][ 2×3 2×4 ]] = [[ 2 4 ][ 6 8 ]]

    The other scalar multiplication, to find –1A, works the same way:

      -1A = -1 × [[ 1 2 ][ 3 4 ]] = [[ -1×1 -1×2 ][ -1×3 -1×4 ]] = [[ -1 -2 ][ -3 -4 ]]

    So the final answer is:   Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

      2A = [[ 2 4 ][ 6 8 ]]

      -1A = [[ -1 -2 ][ -3 -4 ]]

Scalar multiplication is easy. Matrix multiplication, however, is quite another story. In fact, it's a royal pain. Your text probably gave you a complex formula for the process, and that formula probably didn't make any sense to you. That's okay. The process is messy, and that complicated formula is the best they can do for an explanation in a formal setting like a textbook. Here's how the process works:

  • Find the product AB for the following matrices:

      • A = [[ 1 0 -2 ][ 0 3 -1 ]] , B = [[ 0 3 ][ -2 -1 ][ 0 4 ]]

    To calculate AB, I write down A and B next to each other like this:

      [[ 1 0 -2 ][ 0 3 -1 ]] × [[ 0 3 ][ -2 -1 ][ 0 4 ]]

    Now I need to multiply the ROWS of A by the COLUMNS of B. By this I mean that I first take the first row of A and the first column of B, and I multiply the first entries, then the second entries, and then the third entries, and then I add the three products. The sum is one entry in the product matrix AB; in fact, being the product of row 1 and column 1, the result is the 1,1-entry of AB. Then I continue in like manner. For instance, the sum of the products from row 2 of A and column 1 of B is the 2,1-entry of AB.

    When I multiply matrices, I use my fingers to keep track of what I'm doing. The following animation is my attempt to illustrate this process. (Don't laugh; I'm no artist!)

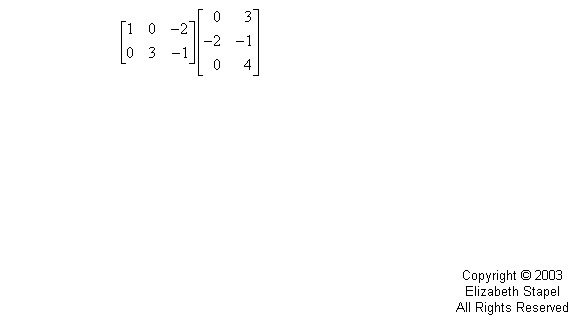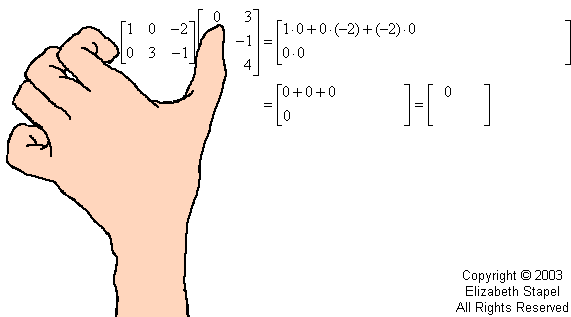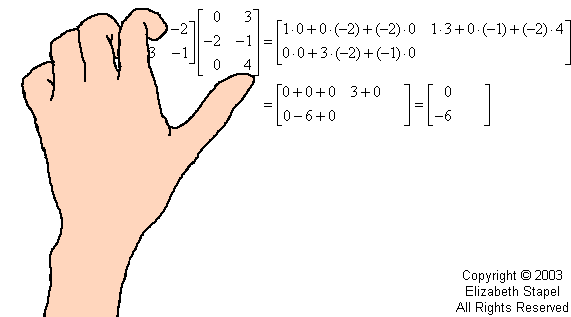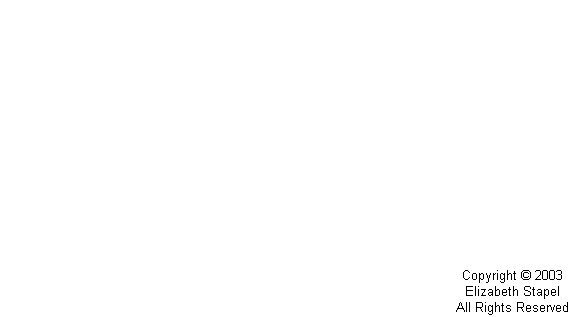
Demonstration of how to use your fingers to keep track of the multiplications.

    (Now, class; what did I say about laughing?)

    The final answer is:

      AB = [[ 0 -5 ][ -6 -7 ]]

As you saw on the above example, the general rule is that the product of the i-th row of A and the j-th column of B is the i,j-th entry of the product matrix AB. This general rule is, in large part, what that complicated formula in your text was all about.

For instance, when I, in the above example, multiplied the first row (of A) and the second column (of B), this gave me the first-row-second-column entry in the product matrix AB.

Top  |  1 | 2 | 3  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Scalar and Matrix Multiplication." Purplemath. Available from
    https://www.purplemath.com/modules/mtrxmult.htm. Accessed
 

 

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

   Copyright © 2021  Elizabeth Stapel   |   About   |   Terms of Use   |   Linking   |   Site Licensing

 

Contact Us