Print-friendly page

The Common and Natural Logarithms (page 3 of 3)

Sections: Introduction to logs, Simplifying log expressions, Common and natural logs

Logs can have any number of bases, but two bases are more useful than the others. For historical reasons, log-base-10 is often used. For instance, pH (the measure of a substance's acidity or alkalinity), decibels (the measure of sound intensity), and the Richter scale (the measure of earthquake intensity) all involve base-10 logs. The base-10 log is usually called "the common log", and is usually written as "log(x)". That is, if there is no base written, you should assume that the base is 10.

(This is similar to the case for radicals, where, if there is no little number in the front of the radical sign, you know that they mean "square root". Just as they do not customarily put the little "2" in for the square root, so also they do not customarily put the little "10" in for the common log.)

The other important log is the "natural", or base-e, log, denoted as "ln(x)" and pronounced as "ell-enn-of-x". Why would "Natural Log" be denoted by "LN", rather than by "NL"? I think it is because Euler ("OY-lur"), the guy who discovered (invented?) the natural exponential, was Swiss and spoke French, which meant that he wasn't calling it "the Natural Log" but "le Logarithme Naturel", in which case, "LN" makes sense. Just as the number e arises naturally in math and the sciences, so also does the natural log arise naturally, which is why you need to be familiar with the natural log.

(If you eventually progress to much-more advanced mathematics, you may find that sometimes "log(x)" means the base-e log, or "ln(x)", rather than the common log. But this would be a long ways down the road; you won't likely encounter this in your studies for a long time, if ever.)

Because these two logs are pretty much the only logs that are used "in real life", these are the only two for which you have calculator keys. Make sure you know where these keys are, and how to use them.

• Simplify log(100).

Since 100 = 10², then log(100) = log(10²) = 2, because "log(100) = y" means "10 ^y = 100 = 10²", so y = 2.

log(100) = 2

Plug "log(100)" into your calculator, and you'll get the same answer.

• Simplify log(98).

Since 98 is not a nice neat power of 10 (the way 100 was), I cannot be clever with exponents to arrive at an exact answer. That is, on this problem, I am stuck with using my calculator to get an approximate value. So I'll plug this into my calculator, remembering to use the "LOG" key (not the "LN" key), and I get log(98) = 1.99122607569..., or:

log(98) = 1.99, rounded to two decimal places

• Simplify ln(e^4.5).

Remember that "ln( )" means the base-e log, so "ln(e^4.5)" might be thought of as "log_e(e^4.5)". The Relationship says that "ln(e^4.5) = y" means "e ^y = e^4.5", so y = 4.5, and:

ln(e^4.5) = 4.5

Plug "ln(e^4.5)" into your calculator, and you'll get the same answer. (Make sure you put parentheses around the "e^4.5", so the calculator knows that the exponent is inside the log.)

• Simplify ln(2).   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

Since 2 is a nice neat whole number and since e isn't, then it is unlikely that 2 is a nice neat power of e. So I can't simplify this expression by being clever with exponents. Instead, I'll have to evaluate this in my calculator, getting an approximate answer of ln(2) = 0.69314718056..., or:

ln(2) = 0.69, rounded to two decimal places.

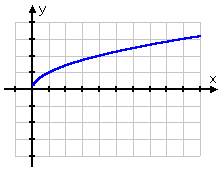
The graph of a logarithm looks similar to that of a square root:

square-root function	log function

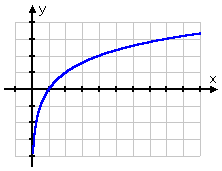
However, the square-root graph stops at the point (0, 0), while the logarithm graph does not pass through the origin, but instead passes through (1, 0) and then continues down along the right-hand (positive) side of the y-axis. Since the log function is the inverse of the exponential function, the graph of the log is the flip of the graph of the exponential:

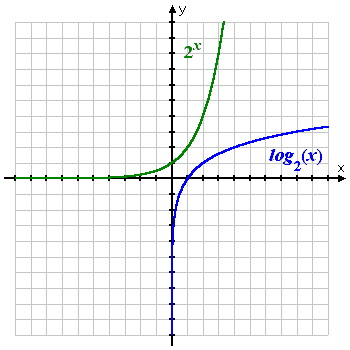
The exponential rides along the top of the x-axis, crosses the y-axis at the point (0, 1), and then shoots up. The logarithm rides up the right side of the y-axis, crosses the x-axis at the point (1, 0), and then shoots right. For more information, review the graphing lesson.

<< Previous  Top  |  1 | 2 | 3  |  Return to Index

  Copyright © 2006-2008  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?