Worked Examples of Linear Programming Word Problems
Purplemath
Sometimes, it may seem like they've given you information that requires more than two variables.
But, if you take your time, you should be able to figure how what the variables should *really* stand for.
Content Continues Below
- In order to ensure optimal health (and thus accurate test results), a lab technician needs to feed the rabbits a daily diet containing a minimum of 24 grams (g) of fat, 36 g of carbohydrates, and 4 g of protien. But the rabbits should be fed no more than five ounces of food a day.
Rather than order rabbit food that is custom-blended, it is cheaper to order Food X and Food Y, and blend them for an optimal mix. Food X contains 8 g of fat, 12 g of carbohydrates, and 2 g of protein per ounce, and costs $0.20 per ounce. Food Y contains 12 g of fat, 12 g of carbohydrates, and 1 g of protein per ounce, at a cost of $0.30 per ounce.
What is the optimal blend?
I need to find the optimal blend of fat, carbs, and protein. Won't that take three variables?
Actually, the exercise is asking for the number of ounces of each food required for the optimal daily blend. So my variables will stand for the number of ounces of each of the two kinds of food:
x: number of ounces of Food X
y: number of ounces of Food Y
Since I can't use negative amounts of either food, the first two constrains are the usual ones: x ≥ 0 and y ≥ 0. The other constraints come from the grams of fat, carbohydrates, and protein per ounce:
fat: 8x + 12y ≥ 24
carbs: 12x + 12y ≥ 36
protein: 2x + 1y ≥ 4
Affiliate
Advertisement
Also, the maximum weight of the food is five ounces, so:
x + y ≤ 5
The optimization equation will be the cost relation C = 0.2x + 0.3y, but this time I'll be finding the *minimum* value, not the maximum.
Putting it all together, my system is:
C = 0.2x + 0.3y, subject to:
x ≥ 0
y ≥ 0
y ≥ −(2/3)x + 2
y ≥ −x + 3
y ≥ −2x + 4
y ≤ −x + 5
This system of linear inequalities graphs as:
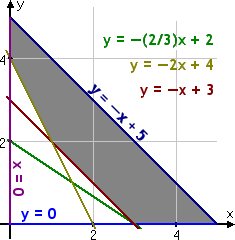
(Note: One of the lines above is irrelevant to the system. Can you tell which one?)
The corners of the above feasibility region are at (0, 4), (0, 5), (3, 0), (5, 0), and (1, 2). When testing these points, remember that you're looking here for the minimum, so you want the point that gives you the smallest result. You should get a minimum cost of sixty cents per daily serving, using three ounces of Food X only.
Content Continues Below
Sometimes you'll have more than just two things to deal with. The next example has three things to juggle. (The next page provides an example of juggling four things.)
- You have $12,000 to invest, and three different funds from which to choose. The municipal bond fund has a 7% return, the local bank's CDs have an 8% return, and the high-risk account has an expected (hoped-for) 12% return.
To minimize risk, you decide not to invest any more than $2,000 in the high-risk account. For tax reasons, you need to invest at least three times as much in the municipal bonds as in the bank CDs. Assuming the year-end yields are as expected, what are the optimal investment amounts?
Since the question is asking me to find the amount of money for each account, my variables will need to stand for those amounts. Since I'd like to deal with smaller numbers, I'll count by thousands, so:
x: amount (in thousands) invested in bonds
y: amount (in thousands) invested in CDs
Um... now what? I only have two variables, but I have three accounts.
To handle this, I need the "how much is left" construction:
12 − x − y: amount (in thousands) invested in the high-risk account
Affiliate
I can't invest negative amounts of money, so the first two constraints are the usual ones: x ≥ 0 and y ≥ 0. The amount in the high-risk account can't be negative either, so 12 − x − y ≥ 0, which rearranges (for graphing) as:
y ≤ −x + 12
Also, the upper limit on the high-risk account gives me the inequality (12 − x − y) ≤ 2. This rearranges as:
y ≥ −x + 10
And the tax requirements says that (the amount in bonds) is at least (three) times (the amount in the certificate of deposit), or:
x ≥ 3y
3y ≤ x
y ≤ (1/3)x
The optimization equation will be the total investment yield Y:
Y = 0.07x + 0.08y + 0.12(12 − x − y)
This rearranges as:
Y = 1.44 − 0.05x − 0.04y
Then the entire system is as follows:
Maximize Y = 1.44 − 0.05x − 0.04y, subject to:
x ≥ 0
y ≥ 0
y ≥ −x + 10
y ≤ −x + 12
y ≤ (1/3)x
The feasibility region graphs as:
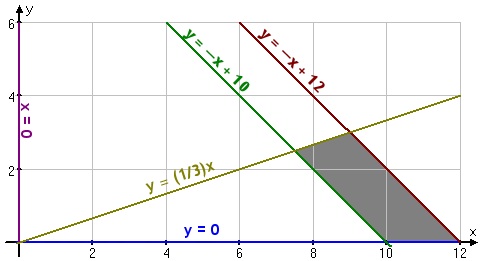
The corner points will be at (9, 3), (12, 0), (10, 0), and (7.5, 2.5). When you plug these into the optimization equation, you should get an optimal return of $965 when you invest $7,500 in municipal bonds, $2,500 in CDs, and the remaining $2,000 in the high-risk account.
URL: https://www.purplemath.com/modules/linprog4.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




