Linear Programming: Word Problems (page 3 of 5)

Sections: Optimizing linear systems, Setting up word problems

• A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators much be shipped each day.

If each scientific calculator sold results in a $2 loss, but each graphing calculator produces a $5 profit, how many of each type should be made daily to maximize net profits?

The question asks for the optimal number of calculators, so my variables will stand for that:

x: number of scientific calculators produced
y: number of graphing calculators produced

Advertisement

Since they can't produce negative numbers of calculators, I have the two constraints, x > 0 and y > 0. But in this case, I can ignore these constraints, because I already have that x > 100 and y > 80. The exercise also gives maximums: x < 200 and y < 170. The minimum shipping requirement gives me x + y > 200; in other words, y > –x + 200. The profit relation will be my optimization equation: P = –2x + 5y. So the entire system is:

P = –2x + 5y, subject to:
100 < x < 200 
80 <  y < 170 
y > –x + 200 


The feasibility region graphs as:   Copyright © Elizabeth Stapel 2006-2011 All Rights Reserved

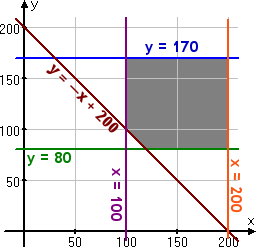
When you test the corner points at (100, 170), (200, 170), (200, 80), (120, 80), and (100, 100), you should obtain the maximum value of P = 650 at (x, y) = (100, 170). That is, the solution is "100 scientific calculators and 170 graphing calculators".

• You need to buy some filing cabinets. You know that Cabinet X costs $10 per unit, requires six square feet of floor space, and holds eight cubic feet of files. Cabinet Y costs $20 per unit, requires eight square feet of floor space, and holds twelve cubic feet of files. You have been given $140 for this purchase, though you don't have to spend that much. The office has room for no more than 72 square feet of cabinets. How many of which model should you buy, in order to maximize storage volume?

The question ask for the number of cabinets I need to buy, so my variables will stand for that:

x: number of model X cabinets purchased
y: number of model Y cabinets purchased

Naturally, x > 0 and y > 0. I have to consider costs and floor space (the "footprint" of each unit), while maximizing the storage volume, so costs and floor space will be my constraints, while volume will be my optimization equation.

cost: 10x + 20y < 140, or y < –( ¹/₂ )x + 7
space: 6x + 8y < 72, or y < –( ³/₄ )x + 9
volume: V = 8x + 12y

This system (along with the first two constraints) graphs as:

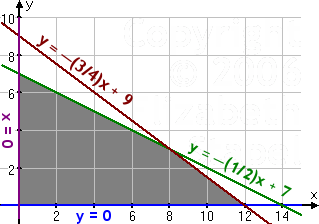
When you test the corner points at (8, 3), (0, 7), and (12, 0), you should obtain a maximal volume of 100 cubic feet by buying eight of model X and three of model Y.

<< Previous  Top  |  1 | 2 | 3 | 4 | 5  |  Return to Index  Next >>

  Copyright © 2006-2014  Elizabeth Stapel   |   About   |   Terms of Use

Contact Us