Print-friendly page

Composition of Functions:
     Composing with Sets of Points (page 1 of 5)

Sections: Composing functions that are sets of point, Composing functions at points, Composing functions with other functions, Word problems using composition, Inverse functions and composition

Until now, given a function  f(x), you would plug a number or another variable in for x. You could even get fancy and plug another whole expression in for x. For example, given  f(x) = 2x + 3, you could find f(y² – 1) by plugging y² – 1 in for x to get f(y² – 1) = 2(y² – 1) + 3 = 2y² – 2 + 3 = 2y² + 1.

In function composition, you're plugging entire functions in for the x. (In other words, you're always getting "fancy"!) But let's start simple. Instead of dealing with functions as formulas, let's deal with functions as sets of (x, y) points:

• Let f = {(–2, 3), (–1, 1), (0, 0), (1, –1), (2, –3)} and
  let g = {(–3, 1), (–1, –2), (0, 2), (2, 2), (3, 1)}. 
   
  Find (i) f (1), (ii) g(–1), and (iii) (g o f )(1).

(i) This type of problem is meant to emphasize that the (x, y) points are really (x, f (x)) points, so, to find  f (1) in this example, you would find the point in the set of f (x) points that has x = 1. Then f (1) is the y-value of that point. In this case, the point in the set of f (x) points with x = 1 is (1, –1), so:

f (1) = –1

(ii) The point in the g(x) set of point with x = –1 is the point (–1, –2), so:

g(–1) = –2

(iii) What is "(g o f )(1)"? This is read as "g compose f of 1", and means "plug 1 into f, evaluate, and then plug the result into g". The computation can feel a lot easier if you use the more intuitive formatting:

(g o f )(1) = g( f(1))

Now work in steps. Note that, while you are used to doing things from the left to the right (because that's how we read), composition works from the right to the left (or, if you prefer, from the inside out). So we'll start with the x = 1. We are plugging this into f(x), so we look in the set of f(x) points for a point with x = 1. The point is (1, –1). This gives us f(1) = –1, so now we have:

(g o f )(1) = g( f(1)) = g(–1)

Working toward the left, we are now plugging x = –1 (from "f(1) = –1") into g(x), so we look in the set of g(x) points for a point with x = –1. The point is (–1, –2). This gives us g(–1) = –2, so now we have the answer:   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

(g o f )(1) = g( f(1)) = g(–1) = –2

Note that they never told us what f(x) or g(x) might be; we were only given a list of points. But this list is sufficient for answering the questions, as long as you keep track of your x- and y-values.

• Let f = {(–2, 3), (–1, 1), (0, 0), (1, –1), (2, –3)} and
  let g = {(–3, 1), (–1, –2), (0, 2), (2, 2), (3, 1)}. 
   
  Find (i) ( f o g)(0), (ii) ( f o g)(–1), and (iii) (g o f )(–1).

(i) To find ( f o g)(0), I'll rewrite:

( f o g)(0) = f(g(0))

So I'm going to plug zero into g(x), and then plug the result into f(x). Looking at the g(x) points, I find (0, 2), so g(0) = 2. Looking at the f(x) points, I find (2, –3), so f(2) = –3. Then:

( f o g)(0) = f(g(0)) = f(2) = –3

(ii) The second part works the same way:

( f o g)(–1) = f(g(–1)) = f(–2) = 3

(iii) I can rewrite the composition as (g o f )(–1) = g( f(–1)) = g(1).

Uh-oh; there is no g(x) point with x = 1, so it is nonsense to try to find the value of g(1). In math-speak, g(1) is not defined!  Then (g o f )(–1) is not defined either. So the answer is:

(g o f )(–1) is undefined.

Part (iii) of the above example points out an important consideration regarding domain and range. It may be that your composed function (the result you get after composing two other functions) will have a restricted domain, or at least a domain that is more restricted than you might otherwise have expected. This will more important when we deal with composing functions symbolically later.

Another question of this type gives you two graphs, rather than sets of points, and has you read the values from the graphs, rather than the lists. For example:

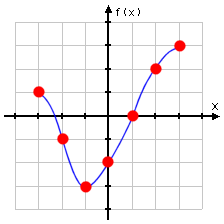
• Given f(x) and g(x) as shown below, find ( f o g)(–1).
     

f(x):	g(x):

In this case, I will read the points from the graph. First, note that ( f o g)(–1) = f(g(–1)). This means that I first need to find g(–1). So I look on the graph of g(x), and find x = –1. Tracing up to the graph of g(x), I see that, for x = –1, y = 3. That is, the point (–1, 3) is on the graph of g(x). So g(–1) = 3.

Now I plug this value, x = 3, into f(x). To do this, I look at the graph of f(x) and find x = 3. Tracing up to the graph of  f(x), I see that, for x = 3, y = 3. That is, the point (3, 3) is on the graph of  f(x). So f(3) = 3.

Then ( f o g)(–1) = f(g(–1)) = f(3) = 3.

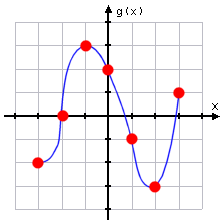
• Given f(x) and g(x) as shown in the graphs below, find ( g o f )(x) for whole-number values of x on the interval –3 < x < 3.
     

f(x):	g(x):

This is asking for all the values of (g o f )(x) = g( f(x)) for whole-valued x between –3 and 3.  So I'll just follow the points on the graphs and compute all the values:

(g o f )(–3) = g( f(–3)) = g(1) = –1

I got this answer by looking at x = –3 on the f(x) graph, finding the corresponding y-value of 1 on the f(x) graph, and using this answer as my new x-value on the g(x) graph. That is, I looked at x = –3 on the f(x) graph, found that this led to y = 1, went to x = 1 on the g(x) graph, and found that this led to y = –1.

(g o f )(–2) = g( f(–2)) = g(–1) = 3
(g o f )(–1) = g( f(–1)) = g(–3) = –2
(g o f )(0) = g( f(0)) = g(–2) = 0
(g o f )(1) = g( f(1)) = g(0) = 2
(g o f )(2) = g( f(2)) = g(2) = –3
(g o f )(3) = g( f(3)) = g(3) = 1

You aren't generally given functions as sets of points or as graphs, however. Generally, you have formulas for your functions. So let's see what composition looks like in that case...

Top  |  1 | 2 | 3 | 4 | 5  |  Return to Index  Next >>

  Copyright © 2006-2008  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?