Print-friendly page

Functions: Domain and Range (page 2 of 2)

Sections: Functions versus relations, Domain and range

Let's return to the subject of domain and range. When functions are first introduced, you will probably have some slightly pathetic "functions" and relations to deal with, being just sets of points. These won't be terribly useful or interesting functions and relations, but your text wants you to get the idea of what the domain and range are. For instance:

• State the domain and range of the following relation. Is the relation a function?
  {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}

This list of points, being a relationship between certain x's and certain y's, is a relation. The domain is all the x-values, and the range is all the y-values. You list the values without duplication:

domain:  {2, 3, 4, 6}

range:  {–3, –1, 3, 6}

(It is customary to list these values in numerical order, but it is not required. Sets are called "unordered lists", so you can list the numbers in any order you feel like. Just don't duplicate: technically, repititions are okay in sets, but most instructions would count off for this.)

While this is a relation (because x's and y's are being related to each other), you have two points with the same x-value: (2, –3) and (2, 3). Since x = 2 gives you two possible destinations, then this relation is not a function.

Note that all I had to do to check whether the relation was a function was to look for duplicate x-values. If you find a duplicate x-value, then the different y-values mean that you do not have a function.

• State the domain and range of the following relation. Is the relation a function?
  {(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}

  List the x-values for the domain and the y-values for the range:

  domain:  {–3, –2, –1, 0, 1, 2}

  range:  {5}   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

This is another example of a "boring" function (like we saw in the first chart higher up in this page), because all the x-values go to the exact same y-value. But each x-value is different, so, while boring, this relation is indeed a function. (In point of fact, these points lie on the horizontal line y = 5.)

There is one other case for finding the domain and range of functions. They will give you a function and ask you to find the domain (and maybe the range, too). I have only ever seen (or can even think of) two things at this stage in your mathematical career that you'll have to check in order to determine the domain of the function they'll give you, and those two things are denominators and square roots.

• Determine the domain and range of the given function:

  

  The domain is all the values that x is allowed to take on. The only problem you have with this function is that you have to be careful not to divide by zero. So the only values that x can not take on are those which would cause division by zero. So set the denominator equal to zero and solve; the domain will be everything else.

  x² – x – 2 = 0
  (x – 2)(x + 1) = 0
  x = 2   or  x = –1

  Then the domain is "all x not equal to –1 or 2".

The range is a bit trickier, which is why they may not ask for it. In general, though, they'll want you to graph the function and find the range from the picture. In this case:

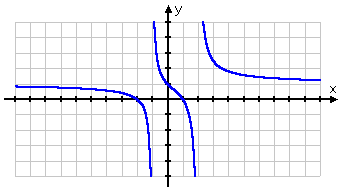
As you can see from the picture, the graph covers all y-values (that is, the graph will go as low as you like, and will also go as high as you like). Since the graph will eventually cover all possible values of y, then the range is "all real numbers".

• Determine the domain and range of the given function:

  

  The domain is all values that x can take on. The only problem you have with this function is that you cannot have a negative inside the square root. So set the insides greater-than-or-equal-to zero, and solve. This will be the domain:

  –2x + 3 > 0
  –2x > –3
  2x < 3
  x < 3/2 = 1.5

  Then the domain is "all x < 3/2".

The range requires a graph. Be sure to be careful when graphing radicals:

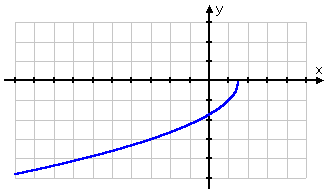
The graph starts at y = 0 and goes down from there. While the graph goes down very slowly, you know that, eventually, you can go as low as you like (by picking an x that is sufficiently big). Also, from your experience with graphing, you know that the graph will never start coming back up. Then the range is "y < 0".

• Determine the domain and range of the given function:

  y = –x⁴ + 4

  This is just a garden-variety polynomial. There are no denominators (so no division-by-zero problems) and no radicals (so no square-root-of-a-negative problems). There are no problems with a polynomial. There are no values that you can't plug in for x. When you have a polynomial, the answer is always that the domain is "all x".

The range will vary from polynomial to polynomial, and they probably won't even ask, but, if they do, look at the picture:

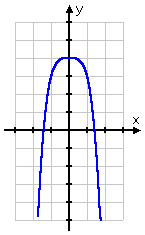
The graph goes only as high as y = 4, but it will go as low as you like. Then:

The range is "all y < 4".

<< Previous  Top  |  1 | 2  |  Return to Index

  Copyright © 2006-2008  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?