Return to the Purplemath home page

 The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra


powered by FreeFind

 

Return to the Lessons Index  | Do the Lessons in Order  |  Get "Purplemath on CD" for offline use  |  Print-friendly page

The Binomial Theorem: Formulas (page 1 of 2)

Sections: The formulas, Worked examples

The Binomial Theorem is a quick way (okay, it's a less slow way) of expanding (or multiplying out) a binomial expression that has been raised to some (generally inconveniently large) power. For instance, the expression (3x – 2)10 would be very painful to multiply out by hand. Thankfully, somebody figured out a formula for this expansion, and we can plug the binomial 3x – 2 and the power 10 into that formula to get that expanded (multiplied-out) form.

The formal expression of the Binomial Theorem is as follows:

    (a + b)^n = sum[k=0,n][(n over k)a^(n-k)b^k]   Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved

Yeah, I know; that formula never helped me much, either. And it doesn't help that different texts use different notations to mean the same thing. The parenthetical bit above has these equivalents:

    (n over k) = nCk = n!/[(n-k)!k!]

Recall that the factorial notation "n!" means " the product of all the whole numbers between 1 and n", so, for instance, 6! = 1×2×3×4×5×6. Then the notation "10C7" (often pronounced as "ten, choose seven") means:

    10_C_7 = 10! / [(10 - 7)! 7!] = 10! / [3!7!] = 120

 

Many calculators can evaluate this "n choose m" notation for you. Just look for a key that looks like "nCm" or "nCr", or for a similar item on the "Prob" or "Math" menu, or check your owner's manual under "probability" or "combinations".

 

 
probability menu on graphing calculator
  

 
The evaluation will probably look something like this:

 

screen capture: 10 nCr 7 = 120
  

 
There is another way to find the value of "nCr", and it's called "Pascal's Triangle". To make the triangle, you start with a pyramid of three 1's, like this:

 

first two rows

  
Then you get the next row of numbers by adding the pairs of numbers from above. (Where there is only one number above, you just carry down the 1.)

 

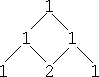
first three rows: (1) (1 1) (1 2 1)

 

Keep going, always adding pairs of numbers from the previous row..

 

 
To find, say, 6C4, you go down to the row where there is a "6" after the initial "1", and then go over to the 5th (not the 4th) entry, to find that 6C4 = 15.

  

(1) (1 1) (1 2 1) (1 3 3 1) (1 4 6 4 1) (1 5 10 10 5 1) (1 6 15 20 15 6 1) ...and so forth.

As you might imagine, drawing Pascal's Triangle every time you have to expand a binomial would be a rather long process, especially if the binomial has a large exponent on it. People have done a lot of studies on Pascal's Triangle, but in practical terms, it's probably best to just use your calculator to find nCr, rather than using the Triangle. The Triangle is cute, I suppose, but it's not terribly helpful in this context, being more time-consuming than anything else. For instance, on a test, do you want to evaluate "10C7" by calculating eleven rows of the Triangle, or by pushing four buttons on your calculator?

I could never remember the formula for the Binomial Theorem, so instead, I just learned how it worked. I noticed that the powers on each term in the expansion always added up to whatever n was, and that the terms counted up from zero to n. Returning to our intial example of (3x – 2)10, the powers on every term of the expansion will add up to 10, and the powers on the terms will increment by counting up from zero to 10:

    (3x – 2)10 = 10C0 (3x)10–0(–2)0 + 10C1 (3x)10–1(–2)1 + 10C2 (3x)10–2(–2)2

      + 10C3 (3x)10–3(–2)3 + 10C4 (3x)10–4(–2)4 + 10C5 (3x)10–5(–2)5

      + 10C6 (3x)10–6(–2)6 + 10C7 (3x)10–7(–2)7 + 10C8 (3x)10–8(–2)8

      + 10C9 (3x)10–9(–2)9 + 10C10 (3x)10–10(–2)10

Note how the highlighted counter number counts up from zero to 10, with the factors on the ends of each term having the counter number, and the factor in the middle having the counter number subtracted from 10. This pattern is all you really need to know about the Binomial Theorem; this pattern is how it works.

Your first step, given a binomial to expand, should be to plug it into the Theorem, just like I did above. Don't try to do too many steps at once. Only after you've set up your binomial in the Theorem's pattern should you start to simplify the terms. The Binomial Theorem works best as a "plug-n-chug" process, but you should plug in first; chug later. I've done my "plugging" above; now "chugging" gives me:

    (1)(59049)x10(1) + (10)(19683)x9(–2) + (45)(6561)x8(4) + (120)(2187)x7(–8)

      + (210)(729)x6(16) + (252)(243)x5(–32) + (210)(81)x4(64)

      + (120)(27)x3(–128) + (45)(9)x2(256) + (10)(3)x(–512) + (1)(1)(1)(1024)

    = 59049x10 – 393660x9 + 1180980x8 – 2099520x7 + 2449440x6 – 1959552x5

      + 1088640x4 – 414720x3 + 103680x2 – 15360x + 1024

As painful as the Binomial-Theorem process is, it's still easier than trying to multiply this stuff out by hand. So don't let the Formula put you off. It's just another thing to memorize, so memorize it, at least for the next test. The biggest source of errors in the Binomial Theorem (other than forgetting the Theorem) is the simplification process. Don't try to do it in your head, or try to do too many steps at once. Write things out nice and clearly, as I did above, so you have a better chance of getting the right answer. (And it would be good to do a bunch of practice problems, so the process is fairly automatic by the time you hit the next test.)

Top  |  1 | 2  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "The Binomial Theorem: Formulas." Purplemath. Available from
    http://www.purplemath.com/modules/binomial.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  Donating
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

This lesson may be printed out for your personal use.

Content copyright protected by Copyscape website plagiarism search

  Copyright © 1999-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

 Feedback   |   Error?