Reference Angles & Trig Values
Purplemath
There are a few (a very few) angles that spit out relatively "neat" trigonometric values, involving, at worst, one square root. Because of their relatively simple values, these are the angles which will typically be used in math problems (in calculus, especially), and you will be expected to know these value by heart.
Usually, textbooks present this short list of values in a table that you are expected to memorize. But pictures are generally easier to recall (on tests, etc) than tables, so this lesson will show the way in which many people really keep track of these values.
How do I find the trig values for 45° angles?
To find (or recall) the trig values for 45° angles:
- Draw a 45-45-90 triangle with short sides having lengths of either (a) sqrt(2) or (b) 1.
- Label the hypotenuse as having a corresponding length of either (a) 2 or (b) sqrt(2).
- From whichever triangle you have drawn (either Triangle (a) or Triangle (b)), read off the trig ratio you need.
Expanding on the above a bit, if you need a trigonometric value for a 45-degree angle, then you can start by drawing either of the 45-45-90-degree triangles shown below, labelling the two short legs as having lengths of 1, and the hypotenuse having a length of :
| Triangle (a) | Triangle (b) |
 |
 |
Why are there two different ways of setting up this triangle? Because some instructors don't want any square roots in the denominators for 45°-angle trig values; for that instructor, you'd use Triangle (a). But other instructors, and certainly those in later courses (like calculus) won't care about radicals in the denominators; they'd prefer you use the "simplified" ratios generated by Triangle (b). (I use Triangle (b) in my own computations.) So let's do the two cases. (In each case, the angle symbol used, which looks in the pictures above kind of like a zero with a line across it, is the Greek letter theta, pronounced "THAY-tuh".)
Triangle (a) is one whose values you'll just have to memorize, if it's the one you're supposed to be using (that is, if you're not allowed to have radicals in the denominator). Label the two matching legs as being of length sqrt(2). Then the Pythagorean Theorem says that the hypotenuse must have a length of 2. Then you can read off the trigonometric values you need.
For instance, if you needed to find the tangent (which is "opposite over adjacent"), you would form the ratio sqrt(2)/sqrt(2) = 1, which is the correct value for the tangent. The values of the sine and cosine for a 45° angle are the same; sin(θ) = sqrt(2)/2 and cos(θ) = sqrt(2)/2. If you need to find one of the co-functions (such as cosecant), you may be required to rationalize some denominators.
Triangle (b) is, in my experience, the easier one to work with. For a start, the equal-length legs have a length of one unit — this is a simpler value — and then we get a length of sqrt(2) for the hypotenuse by using the Pythagorean Theorem.
If, for a given exercise, they only want the trigonometric value of the angle, then just read it off the triangle: the sine of θ is (opposite) over (hypoteneuse), or 1/sqrt(2); the cosine of theta is (adjacent) over (hypoteneuse), or 1/sqrt(2); and the tangent of theta is (opposite) over (adjacent), or 1/1 = 1.
Note: It is irrelevant what are the lengths of the actual triangle you are dealing with when you're needing to find trig values; the reference triangle you use will give you the necessary and correct ratios, and thus the correct trigonometric values. I guess the point here is that, whatever is the fraction or ratio that you get from a particular 45° triangle, it will always simplify down to what you get from the reference Triangles above. You can find anything you need from the reference Triangle of your choice. If trying to memorize an entire table isn't working for you, instead simply memorize the triangle of your choice.
And don't worry if your triangle (as printed in the textbook, say, when you're doing your homework) isn't oriented in the same way. The trigonometric values for the 45° angle will always be the same. (If you've gotten as far as working with angles in other quadrants, then use the reference triangle to find the necessary value, and then do a sign change, if necessary.)
How do I find the trig values for 30°- and 60°-angles?
To find (or recall) the trig values for 30° and 60° angles:
- Draw an equilateral triangle having sides of length 2.
- Drop the altitude line from the peak to the midpoint of the base, forming two smaller triangles.
- Relabel the base as now have two lengths of 1.
- Label the various angles and the altitude with their values.
- From the appropriate triangle, read off the trig ratio you need.
Now let's flesh out those steps a bit, shall we? For either of the 30°- and 60°-angles, the triangle below is what you start with:
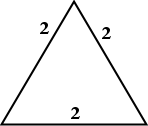
This is a 60-60-60 triangle (that is, an equilateral triangle), with all sides having a length of two units.
Drop the vertical bisector from the top angle down to the bottom side. Note that this bisector is also the altitude (that is, the height) of the triangle.
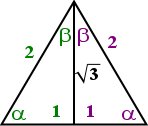
The Pythagorean Theorem tells us that the length of the bisector is sqrt(3). Because the bisector, by definition, cut the angle at the peak in half, it has thus formed two 30-60-90 triangles.
If you are working with a 60° triangle, use the angle labelled above using the Greek letter "alpha" (the funny-looking "a" in the lower corner); if you are doing a 30-degree triangle, use the angle labelled with the Greek letter "beta" (the funny-looking "b" in the upper corner).
In other words, for working with 60° angles, your picture is this half of the triangle:
...and for 30-degree angles, your picture is rotated as shown below:
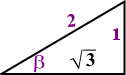
You find trigonometric values and ratios with the 30° and 60° triangles in the exact same manner as with the 45° triangle (ya know: SOH CAH TOA).
What if I'm not allowed to draw pictures to find the angle values?
If your instructor doesn't want you drawing pictures to help you remember the trigonometric values, then... don't let your instructor know that you're drawing the pictures. Use scratch paper that you don't hand in, or draw on the test with something that is cleanly erasable; plus, if you can, write over that area after erasure with something else, to further obfuscate.
(Obfuscation is actually a "real world" skill, in various incarnations.)
It may be that your instructor feels that you're supposed to have everything memorized by now, so pictures are banned. Well, this is why your pencil has an eraser. My Calculus II instructor (an otherwise righteous dude) said that if we drew one of those pictures when working a question on our tests, the entire question would be counted wrong; draw a picture, get a zero. I drew the pictures anyway, but very lightly, in pencil, and erased them all before I handed the tests in. I might do the picture-drawing scratch-work for Question 12 in the space for Question 13, which I'd later overwrite (after erasure). He never knew the difference, and I passed the course. You do what you gotta do.
A helpful (shorthand) table of values
While many people like pictures, some people do prefer tables and charts. If tables work better for you, then this table comes highly recommended, having been "field-tested" by a working instructor:
| angle measure: | 30° | 45° | 60° | |
| sine | √ | 1 | 2 | 3 |
| cosine | √ | 3 | 2 | 1 |
| divided by 2 | ||||
To find, say, the sine of forty-five degrees, you would start in the "sine" row and grab the square-root symbol (that is, the "√") as you move right to the "45°" column. You would find the 2, giving you now . Then you'd continue on out the bottom of the table, reminding you to include the "divided by 2", to get as your answer. (Note: This can be, and may be required to be, restated as . Ask your instructor now, before the next test, if you're not sure which is preferred.)
The neat pattern of "1, 2, 3" and "3, 2, 1" across the middle rows is meant to help you memorize the table values. Note: Keep in mind that the square root of 1 is just 1, so, for instance, .
Finding angle values on your hand
If you don't mind your classmates watching you count on your fingers (and why should you?), then there is a way to find the values of 0°, 30°, 45°, 60° and 90° angles on your hand. I won't reinvent the wheel so, if you'd like to use that method, then a guy going by the handle "StephenwithaPhD" has an article here. (If you ever take a class where you have to multiply things called "vectors", the whole class will be waving their hands in the air for the Right-Hand Rule, so don't be shy if you want to use your fingers now!)
© 2024 Purplemath, Inc. All right reserved. Web Design by 