Systems of Non-Linear Equations:
    Solving Simple Systems (page 3 of 6)

To find the exact solution to a system of equations, you must use algebra. Let's look at that first system again:

• Solve the following system algebraically:

y = x²
y = 8 – x²

Since I am looking for the intersection points, I am therefore looking for the points where the equations overlap, where they share the same values. That is, I am trying to find any spots where y = x² equals y = 8 – x²:

y = x² = y = 8 – x²

The algebra comes in when I manipulate useful bits of this last equation. I can pick out whichever parts I like. (They're all equal, after all -- at least at the intersection points, but the intersection points are the only points that I care about anyway!) So I can pick out any of the following:

y = x²
y = 8 – x²
y = y
x² = 8 – x²

Each of these sub-equations is true, but only the last one is usefully new and different:

x² = 8 – x²

I can solve this for the x-values that make the equation true:

x² = 8 – x²
2x² = 8
x² = 4
x = –2, +2

Then the solutions to the original system will occur when x = –2 and when x = +2.

Advertisement

What are the corresponding y-values? To find them, I plug the x-values back in to either of the two original equations. (It doesn't matter which one I pick because I only care about the points where the equations spit out the same values. So I can pick whichever equation I like better.) I'll plug the x-values into the first equation, because it's the simpler of the two:

x = –2:

y = x²
y = (–2)² = 4

x = +2:

y = x²
y = (+2)² = 4

Then the solutions (as we already knew) are (x, y) = (–2, 4) and (2, 4).

In the above example, the solutions were nice, "neat" integer values; no fractions or decimals. But solutions will not always be neat, so, while the pictures can be very useful for giving you a "feel" for what is going on, graphing is not as accurate as doing the algebra.

Warning: Students are often taught nowadays to "round" absolutely everything, and are thus implicitly taught that all answers will be "neat" answers. But this is wrong; don't fall for it!

For instance:

• Solve the following system:

y = x² + 3x + 2
y = 2x + 3

I can solve this in the same manner as we did on the previous problem. The "solution" to the system will be any point(s) that the lines share; that is, any point(s) where the x-value and corresponding y-value for y = x² + 3x + 2 is the same as the x-value and corresponding y-value for y = 2x + 3; that is, where the lines overlap or intersect; that is, where y = x² + 3x + 2 equals y = 2x + 3.  Copyright © 2002-2011 Elizabeth Stapel All Rights Reserved

Looking at the graph of the system:
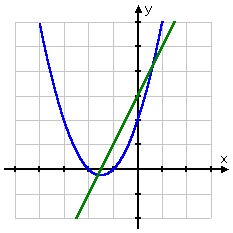
...I can see that there appear to be solutions at around (x, y) = (–1.5, –0.25) and (x, y) = (0.5, 4.25).  But I cannot assume that this is the answer!  The picture can give me a good idea, but only the algebra can give me the actual answer.
I'll set the right-hand sides of the two equations equal to each other, and solve:		x2 + 3x + 2 = 2x + 3 x2 + x – 1 = 0

Using the Quadratic Formula gives me:
Then I have one solution:
...which has a corresponding  y-value of:
The other solution (from the "±" in front of the square root) is:
....which gives me a y-value of:
So the solutions are:

For purposes of graphing, the approximate solutions are:

(x, y) = (–1.62, –0.24) and (0.62, 4.24).

In other words, while my guess from the picture was close, it was not entirely correct nor "exact".

(Note: If the algebra had given me answers that are far afield of these picture-based guesses, I would have been able to safely assume that I had messed up the math somewhere. In this way, the graph can be very helpful for checking your work.)

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index  Next >>

  Copyright © 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

Contact Us