The Slope of a Straight Line
Purplemath
One of the most important properties of a straight line is in how it angles away from the horizontal. This concept is reflected in something called the "slope" of the line.
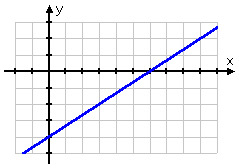
Let's take a look at the straight line . Its graph looks like this:
Content Continues Below
To find the slope, we will need two points from the line.
I'll pick two x-values, plug them into the line equation, and solve for each corresponding y-value. If, say, I pick x = 3, then:
Now let's say I pick x = 9; then:
(By the way, I picked those two x-values precisely because they were multiples of three; by doing so, I knew I'd be able to clear the denominator of the fraction so I'd end up with nice, neat integers for my resulting y-values. It's not a rule that you have to do that, but it's a helpful technique.)
So the two points I found, (3, −2) and (9, 2), are on the line .
To find the slope, designated by "m", we can use the following formula:
(Why "m" for "slope", rather than, say, "s"? The official answer is: Nobody knows.)
Advertisement
In case you haven't encountered those lower-than-the variables numbers before, they're called "subscripts". Subscripts are commonly used to differentiate between similar things, or to count off, for instance, in sequences. In the case of the slope formula, the subscripts merely indicate that we have a "first" point (whose coordinates are subscripted with a "1") and a "second" point (whose coordinates are subscripted with a "2"). In other words, the subscripts indicate nothing more than the fact that we have two points that we're working with.
Affiliate
(It is entirely up to you which point you label as "first" and which you label as "second". As logic dictates, the angle of the line isn't going to change just because you looked at the two points in a different order.)
For computing slopes with the slope formula, the important thing is that we are careful to subtract the x's and y's in the same order. For our two points, if we choose (3, −2) to be our "first" point, then we get the following:
The first y-value above, the −2, was taken from the point (3, −2) ; the second y-value, the 2, came from the point (9, 2); the x-values 3 and 9 were taken from the two points in the same order.
If, on the other hand, we had taken the coordinates from the points in the opposite order, the result would have been exactly the same value:
As you can see, the order in which you list the points really doesn't matter, as long as you subtract the x-values in the same order as you subtracted the y-values. Because of this, the slope formula can be written as it was above, or alternatively it can also be written as:
Let me emphasize this point:
It does not matter which of the two "slope" formulas you use, nor does it matter which point you pick to be your "first" and which you pick to be your "second". The only thing that matters is that you subtract your x-values in the same order as you had subtracted your y-values.
For those who are interested, the equivalence of the two slope formulas above can be proved by noting the following:
y1 − y2 = y1 + (−y2)
= −y2 + y1
= −y1 − (−y2)
= −(y2 − y1)
In the same way:
x1 − x2 = x1 + (−x2)
= −x2 + x1
= −x1 − (−x2)
= −(x2 − x1)
Then the first formula converts to the second one as follows:
As you can see above, doing the subtraction in the so-called "wrong" order serves only to create two "minus" signs which then cancel out. The upshot: Don't worry too much about which point is the "first" point, because it really doesn't matter. (And please don't send me an e-mail claiming that the order does somehow matter, or that one of the above two formulas is somehow "wrong". If you think I'm wrong, then plug pairs of points into both formulas and try to prove me wrong! And keep on plugging until you "see" that the mathematics is in fact correct.)
Content Continues Below
Let's return to the line , and find some more points for it. If I let x = −3, then:
If I let x = 0, then:
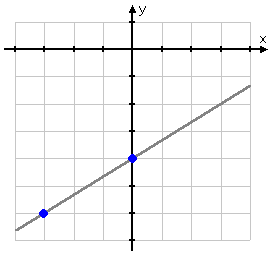
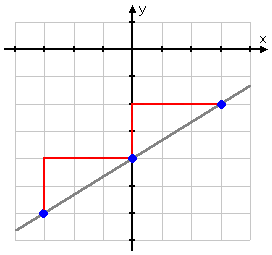
This gives me the two points, (−3, −6) and (0, −4). If I plot these two points on the line, I get the two blue dots shown below:
If I stair-step up from the first point to the second (as I move to the right along the x-axis), I get this:
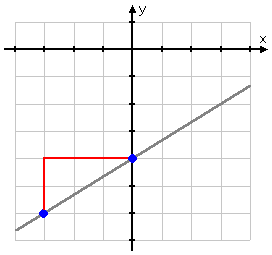
The next point I'll use is (3, −2). Plotting the point and drawing the stair-stepping, I get:
Affiliate
Now take a good look at those stair-steps. Count them off against the grid visible in the background. You'll see that, in going from one plotted point to the next, I moved two steps up and three steps over. In terms familiar to the construction industry, these stair-steps have a (vertical) "rise" of 2 and a (horizontal) "run" of 3. When people refer to "slope" as being "rise over run", this is what they mean. (For more information, try here.)
Affiliate
Let's find the slope of another line equation:
-
Find the slope of y = −2x + 3
Graphing the line, it looks like this:

I'll pick a couple of values for x, and find I'll find the corresponding values for y. Picking x = −1, I get:
y = −2(−1) + 3 = 2 + 3 = 5
Picking x = 2, I get:
y = −2(2) + 3 = −4 + 3 = −1
Then the points (−1, 5) and (2, −1) are on the line y = −2x + 3. The slope of the line is then calculated as:
By the way, if you look at the graph and start with any point on the line (pick one that also lies on the grid, for simplicity's sake), you'll note that the stair-stepping is downward. You go down two, over one; down two, over one; down two, over one. And this matches the slope we found above:
-
Find the slope of the line passing through the points (−3, 5) and (4, −1).
In this case, I don't have to find the points, because they've already given them to me. So I'll go straight to plugging into the formula:
You can use the Mathway widget below to practice finding the slope through a pair of points. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's. (Or skip the widget, and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Clicking "Tap to view steps" will take you directly to the Mathway site, if you'd like to check out their software or get further info.)
URL: https://www.purplemath.com/modules/slope.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()