The Quadratic Formula: Solutions and the Discriminant
Purplemath
Let's do some more examples.
-
Solve x (x − 2) = 4. Round your answer to two decimal places.
I not only cannot apply the Quadratic Formula at this point, I cannot factor either. Why? Because this equation is yet in the correct form.
And I certainly can not claim, with a straight face, that "x = 4, x − 2 = 4", because this is not how "solving by factoring" works.
No matter which solution method I intend to use — whether I'm factoring or using the Quadratic Formula to find my answers — I must first rearrange the equation into the form "(quadratic) = 0".
Content Continues Below
The first thing I'll do here is multiply through on the left-hand side, and then I'll move the 4 over from the right-hand side to the left-hand side:
x (x − 2) = 4
x2 − 2x = 4
x2 − 2x − 4 = 0
Since there are no factors of (1)(−4) = −4 that add up to −2, then this quadratic does not factor. (In other words, there is no possible way that the faux-factoring solution of "x = 4, x − 2 = 4" could be even slightly correct.)
So factoring won't work, but I can use the Quadratic Formula; in this case, I'll be plugging in the values a = 1, b = −2, and c = −4:
Then the answer is:
x = −1.24, x = 3.24, rounded to two decimal places.
For reference, here's what the graph of the associated quadratic, y = x2 − 2x − 4, looks like:
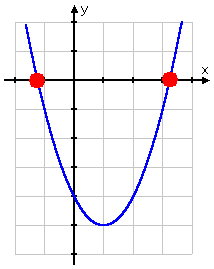
As you can see, the solutions from the Quadratic Formula match up with the x-intercepts. The locations where the graph crosses the x-axis give the values that solve the original equation.
Affiliate
Advertisement
There is another connection between the solutions from the Quadratic Formula and the graph of the parabola: you can tell how many x-intercepts you're going to have from the value inside the square root. The argument (that is, the contents) of the square root, being the expression b2 − 4ac, is called the "discriminant" because, by using its value, you can "discriminate" between (that is, be able to tell the difference between) the various solution types.
In this case, the value of the discriminant b2 − 4ac was 20; in particular, the value was not zero and was not negative. Because the value was not negative, the equation was going to have at least one (real-valued) solution; because the value was not zero, the two solutions were going to be distinct (that is, they were going to be different from each other).
-
Solve 9x2 + 12x + 4 = 0. Leave your answer in exact form.
Using a = 9, b = 12, and c = 4, the Quadratic Formula gives me:
Then the answer is:
In the first example on this page, I had gotten two solutions because the value of the discriminant (that is, the value inside the square root) was non-zero and positive. As a result, the "plus-minus" part of the Formula gave me two distinct values; one for the "plus" part of the numerator and another for the "minus" part. In this case, though, the square root reduced to zero, so the plus-minus didn't count for anything.
This sort of solution, where you get only one value because "plus or minus zero" didn't change anything, is called a "repeated" root, because x is equal to , but it's equal to this value kind-of twice: and .
Content Continues Below
You can see this repetition better if you factor the quadratic (and, because the solutions were nice neat fractions, the quadratic must factor): 9x2 + 12x + 4 = (3x + 2)(3x + 2) = 0, so the first factor gives us 3x + 2 = 0 so , and (from the second, identical factor) 3x + 2 = 0 so again.
Any time you end up with zero inside the square root of the Quadratic Formula, you'll only get one solution to the equation, in the sense of getting one number that solves the equation. But you'll get two solutions, in the sense of the one value being counted twice. In other words, a discriminant (that is, the expression b2 − 4ac) with a value of zero means that you'll get one "repeated" solution value.
Below is what the graph of the associated function, y = 9x2 + 12x + 4, looks like:
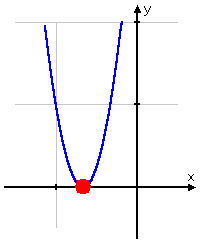
The parabola only just touches the x-axis at ; it doesn't actually cross. This relationship is always true: if you have a root that appears exactly twice (or, which is the same thing, if you get zero inside the square root), then the graph will "kiss" the axis at the solution value, but it will not pass through the axis.
-
Solve 3x2 + 4x + 2 = 0
Since there are no factors of (3)(2) = 6 that add up to 4, this quadratic does not factor. But the Quadratic Formula always works; in this case, I'll be plugging in the values a = 3, b = 4, and c = 2:
At this point, I have a negative number inside the square root. If you haven't learned about complex numbers yet, then you would have to stop here, and the answer would be "no solution"; if you do know about complex numbers, then you can continue the calculations:
Thus, depending upon your level of study, your answer will be one of the following:
real-number solutions: no solution
complex-number solutions:
Affiliate
But whether or not you know about complexes, you know that you cannot graph your answer, because you cannot graph the square root of a negative number on the regular Cartesian place. There are no such values on the x-axis. Since you can't find a graphable solution to the quadratic, then reasonably there should not be any x-intercepts (because you can graph an x-intercept).
Here's the graph of the associated function, y = 3x2 + 4x + 2:

As you can see, the graph does not cross, or even touch, the x-axis. This relationship is always true: If you get a negative value inside the square root, then there will be no real number solution, and therefore no x-intercepts. In other words, if the the discriminant (being the expression b2 − 4ac) has a value which is negative, then you won't have any graphable zeroes.
(The relationship between the discriminant (being the value inside the square root), the type of solutions (two distinct solutions, one repeated solution, or no graphable solutions), and the number of x-intercepts on the graph (two, one, or none) is summarized in a chart on the next page.)
URL: https://www.purplemath.com/modules/quadform2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()