Multiplying Binomials: "foil" (and a warning)
Purplemath
What is "foil"?
foil is a special method of polynomial multiplication, useful ONLY for a two-term polynomial times another two-term polynomial. The letters f-o-i-l come from the words "first", "outer", "inner", "last", and are a memory device for helping you remember how to multiply horizontally, without having to write out the distribution like I did on the previous page, and without dropping any terms or signs.
Below is a graphic displaying what foil stands for:
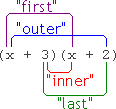
In other words, foil tells you to multiply the first terms in each of the parentheses, then multiply the two terms that are on the "outside" (that is, the two terms which are furthest from each other), then the two terms that are on the "inside" (that is, the two terms which are closest to each other), and then the last terms in each of the parentheses.
Using the example from the previous page, foil works like this:
- Use foil to simplify (x + 3)(x + 2)
Okay; the instructions specify the method I have to use, so here goes:
"first": (x)(x) = x2
"outer": (x)(+2) = +2x
"inner": (+3)(x) = 3x
"last": (+3)(+2) = +6
Adding the results of the four multiplications together, and combining the two "like" terms in the middle, I get:
x2 + 2x + 3x + 6
x2 + 5x + 6
This is the same answer as we got when we multiplied horizontally and vertically.
Many instructors in later math classes come to hate "foil" because it often seems to serve mostly to confuse students when they reach more advanced material. Unfortunately, foil tends to be taught in earlier algebra courses as "the" way to multiply all polynomials, which is clearly not true. (As soon as either one of the polynomials has more than a "first" and "last" term in its parentheses, you're hosed if you try to use Ffoil, because those terms won't "fit".)
And foil is, essentially, just a means of keeping track of what you're doing when you're multiplying horizontally. But, for multiplications of larger numbers, you already know that vertical is the way to go. It's the same in algebra. When multiplying larger polynomials, just about everybody switches to vertical multiplication; it's just so much easier to use.
If you want to use foil, that's fine, but (warning!) keep its restriction in mind: you can ONLY use it for the special case of multiplying two binomials. You can NOT use it at ANY other time!
- Simplify (x − 4)(x − 3)
The instructions don't tell me what method I have to use for this multiplication, so I'll go vertical:
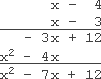
So my answer is:
x2 − 7x + 12
Using foil would give the same answer:
"first": (x)(x) = x2
"outer": (x)(−3) = −3x
"inner": (−4)(x) = −4x
"last": (−4)(−3) = +12
result: (x2) + (−3x) + (−4x) + (+12)
x2 − 7x + 12
But multiplying vertically takes less time, space, and care than does multiplying with foil. When I first encountered vertical multiplication of polynomials, I immediately switched to this method.
- Multiply and simplify: (x − 3y)(x + y)
This multiplication looks like it might be more complicated, because of the second variable, but the process doesn't care how many terms have variables. So I can proceed as usual.
Vertical multiplication gives me this:
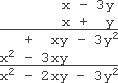
So my hand-in answer is:
x2 − 2xy − 3y2
Using foil would give me:
"first": (x)(x) = x2
"outer": (x)(y) = xy
"inner": (−3y)(x) = −3xy
"last": (−3y)(y) = −3y2
result: (x2) + (xy) + (−3xy) + (−3y2)
x2 − 2xy − 3y2
-
Multiply and simplify: (2x − 5)(3x + 4)
This multiplication has some slightly larger coefficients, but the process is the same. I'll work vertically:
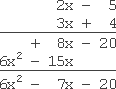
answer: 6x2 − 7x − 20
I won't bother doing the foil process for this exercise.
-
Multiply: (−4x − 1)(5x − 7)
The factors in this product have a lot of "minus" signs, but the process remains the same:
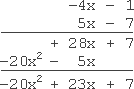
answer: −20x2 + 23x + 7
-
Expand: (x − 3)2
Some students will try to take a shortcut with this and, thinking that the power somehow "distributes" over the terms, they'll square each of the terms (getting an x2 and a 9, but no middle terms with x's in them) and... then they'll be confused about what signs should go where.
Instead, I'm going to write out the square explicitly; the expression they gave me means the following:
(x − 3)(x − 3)
This multiplies as follows:
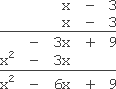
answer: x2 − 6 + 9
-
Expand and simplify:
Fractions? Really?!? Well, the process will work just the same with fractions as it did with whole numbers:
![x + 1/3 is placed above x + 1/2; first row: 1/2 times 1/3 is 1/6, carried down below the 1/2; 1/2 times x is (1/2)x, carried down below the x; second row: x times 1/3 is (1/3)x, carried down below the (1/2)x; x times x is x^2, carried down to the left of the (1/3)x; adding down: (x^2) + [(1/2)x] + [(1/3)x] + 1/6](polys/mult14.png)
Off to the side on my scratch-paper, I add the fractions for the middle term:
So my simplified answer is:
Before we move on, please allow me reiterate what I said at the beginning of this page: "foil" works ONLY for the specific and special case of a two-term expression times another two-term expression. It does NOT apply in ANY other case. You should not rely on foil for general multiplication, and should not expect it to "work" for every multiplication, or even for most multiplications. If you only learn foil, you will not have learned all you need to know, and this will cause you problems later on down the road.
Yes, I'm ranting. But I have seen too many students be greatly hampered in their studies by an unthinking over-reliance on foil. Their instructors often never even taught them any method for multiplying other sorts of polynomials.
For your own sake, take the time to read the next page and learn how to multiply general polynomials properly.
© 2024 Purplemath, Inc. All right reserved. Web Design by 