The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

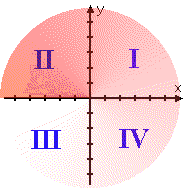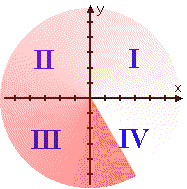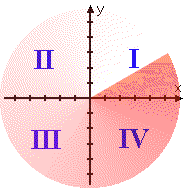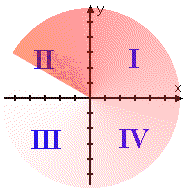
The Quadrants of the Cartesian Plane (page 3 of 3)

Sections: Introduction to the plane, Plotting points, The four quadrants

The two axes divide the plane into four sections called "quadrants". The quadrants are labelled with Roman numerals (not Arabic numerals), starting at the positive x-axis and going around anti-clockwise:

When you get to trigonometry, this method of numbering the quadrants will make perfect sense and will be very useful. For now, just memorize the information. You'll probably have only a few questions on quadrants, and then you'll hardly see the topic again until trigonometry. Typical questions are generally similar to the following:   Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved

• In which quadrant is the point (–2, –3)?

The simplest way for me to answer this is to plot the point:

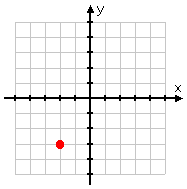
Now I can see that the point (–2, –3) is in Quadrant III.

• In which quadrant is the point (4, y)?

Since they don't tell me what the value of "y" is, then y can be anything. This means that (4, y) is not just one point! Since y can be –5, then (4, –5) is a valid answer. So is (4, –3), (4, 0), (4, 2), and (4, 4). So is any point that has x = 4:

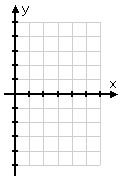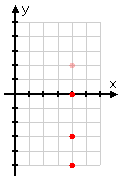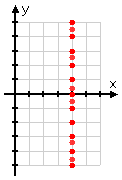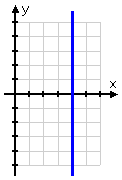
By plotting a bunch of points that "work", I can see that the "point" (4, y) is actually an entire line: the line "x = 4", which passes through two quadrants! So my answer is:


Quadrants I and IV.

By the way, please use standard notation. You can maybe abbreviate "Quadrant" as "Q", but don't completely omit it; use Roman "I, II, III, IV", not Arabic "1, 2, 3, 4"; and use "&" or "and", not "plus" or "+".

• In which quadrant is / are the point(s) (x, y), such that  xy < 0?

This is asking me for a description of the points (x, y), where the coordinate x and y have values such that, when I multiply x and y together, I will get a negative number. To figure this one out, it's probably simplest if I just pick a sample point from each quadrant and see what I get.

In Quadrant I, I'll pick, say, (2, 3). The product of the coordinates is 2 × 3 = 6, which is positive (greater than zero). Since any coordinate product in Quadrant I will be similarly positive, then Quadrant I is not part of my answer.

In Quadrant II, I'll pick, say, (–4, 5). The product is (–4) × 5 = –20, which is negative. Any other coordinate product in Quadrant II will also be negative, so Quadrant II is part of my answer.

In Quadrant III, I'll pick, say, (–2, –1). The product is (–2) × (–1) = 2, which is positive. Any other product in Quadrant III will be positive also, so Quadrant III is not part of my answer.

In Quadrant IV, I'll pick, say, (3, –4). The product is 3 × (–4) = –12, which is negative. Any other product in Quadrant IV will be negative also, so Quadrant IV is part of my answer.

The points (x, y), with xy < 0, lie in Quadrants II and IV.

You can use the Mathway widget below to practice "Points, Lines, and Line Segments", subtopic "Finding a Point's Quadrant". Try the entered exercise, or type in your own exercise. Then click "Answer" to compare your answer to Mathway's.

To activate, click in the "Enter Problem" box below:

(Clicking on "View Steps" on the widget's answer screen will take you to the Mathway site, where you can register for a free seven-day trial of the software.)

<< Previous  Top  |  1 | 2 | 3  |  Return to Index

  Copyright © 2000-2012  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?