Geometry Word Problems: Basic Examples (page 2 of 6)

Sections: Introduction, Basic examples, Triangle formulas, Complex examples, The Box Problem & the Goat Problem, Max / Min problems

Sometimes geometry word problems wrap the geometry in a thick layer of "real life". You will need to be able to "see" the geometry, and extract the relevant information.

• Suppose a water tank in the shape of a right circular cylinder is thirty feet long and eight feet in diameter. How much sheet metal was used in its construction?

What they are asking for here is the surface area of the water tank. The total surface area of the tank will be the sum of the surface areas of the side (the cylindrical part) and of the ends. If the diameter is eight feet, then the radius is four feet. The surface area of each end is given by the area formula for a circle with radius r: A = (pi)r². (There are two end pieces, so I will be multiplying this area by 2 when I find my total-surface-area formula.) The surface area of the cylinder is the circumference of the circle, multiplied by the height: A = 2(pi)rh.

	Side view of the cylindrical tank, showing the radius "r".
	An "exploded" view of the tank, showing the three separate surfaces whose areas I need to find.

Then the total surface area of this tank is given by:

2 ×( (pi)r² ) + 2(pi)rh    (the two ends, plus the cylinder)
    = 2( (pi) (4²) ) + 2(pi) (4)(30)
    = 2( (pi) × 16 ) + 240(pi)
    = 32(pi) + 240(pi)
    = 272(pi)

Since the original dimensions were given in terms of feet, then my area must be in terms of square feet:

the surface area is 272(pi) square feet.

By the way, this is one of those exercises that doesn't translate well into "real life". In reality, the sheet metal has thickness, and adjustments would be required in order to account for this thickness. For example, if you needed to figure out the amount of sheet metal required to create a tank with a certain volume, you'd have to account for the fact that the volume is on the inside, while the surface area is on the outside. Since the walls of a real-world tank have thickness, the real-world answer would not match the "ideal" mathematical one.

• A piece of 16-gauge copper wire 42 cm long is bent into the shape of a rectangle whose width is twice its length. Find the dimensions of the rectangle.

Do I care that the wire is made of copper, or that the wire is a length of sixteen-gauge? No; all I care is that the length is forty-two units, that the units are centimeters, that the rectangle is twice as long in one direction as the other, and that I'm supposed to find the values of each of these directions. I can ignore the other information.

Since the wire is 42 centimeters long, then the perimeter of the rectangle is 42 centimeters. That is:

2L + 2W = 42

I also know that the width is twice the length, so:

W = 2L

Then:   Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved

2L + 2(2L) = 42    (by substitution for W from the above equation)
2L + 4L = 42
6L = 42
L = 7

Since the width is related to the length by W = 2L, then W = 14, and the rectangle is 7 centimeters long and 14 centimeters wide.

• A circular swimming pool with a diameter of 28 feet has a deck of uniform width built around it.  If the area of the deck is 60(pi) square feet, find its width.

I have this situation:

A pool is surrounded by a deck. The pool has radius 14, and the deck has width "d ".

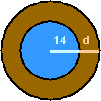
If the diameter of the pool is 28, then the radius is 14. The area of the pool is then:

(pi)r² = (pi)(14)² = 196(pi)

Then the total area of the pool plus the surrounding decking is:

196(pi) + 60(pi) = 256(pi)

Working backwards from the area formula, I can find the radius of the whole pool-plus-deck area:

256(pi) = (pi)r²
256 = r²
16 = r

Since I already know that the pool has a radius of 14 feet, and I now know that the whole area has a radius of 16, then clearly:

the deck is two feet wide.

• If one side of a square is doubled in length and the adjacent side is decreased by two centimeters, the area of the resulting rectangle is 96 square centimeters larger than that of the original square. Find the dimensions of the rectangle.

I'm starting from a square with sides of some unknown length. The sides of the rectangle are defined in terms of that unknown length. So I'll pick a variable for the unknown side-length, create expressions for the rectangle's sides, and then work from there.

square's side length: x
one side is doubled: 2x
next side is decreased by two: x – 2
square's area: x²
rectangle's area: (2x)(x – 2) = 2x² – 4x
new area is 96 more than old area: 2x² – 4x = x² + 96

2x² – 4x = x² + 96
x² – 4x – 96 = 0
(x – 12)(x + 8) = 0
x = 12  or  x = –8

I'm supposed to find the dimensions of a rectangle, so can I just erase that one "minus" sign and say that the rectangle is 12 by 8? No! I defined "x" as standing for the side length of the square, not as one of the sides of the rectangle. Looking back at my definitions, I see what "x = 12" (the only reasonable solution for the square) means that the sides of the rectangle have lengths 2(12) and (12) – 2:

The rectangle measures 24 cm by 10 cm.

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index  Next >>

   Copyright © 2021  Elizabeth Stapel   |   About   |   Terms of Use   |   Linking   |   Site Licensing

Contact Us