Introduction to Negative Numbers
Purplemath
Where did negative numbers come from? Who invented them?
Negative numbers have a long and sometimes contentious history. Mathematicians on the Indian subcontinent had been using negative numbers for a thousand years before Europeans got around to accepting the idea.
Content Continues Below
If you go back far enough, you'll find that some Europeans didn't even necessarily think that 1 was a number.
(We owe our current so-called "Arabic" number system, including the number zero, to Indian mathematicians, too. Previously, Europeans had previously been stuck using Roman numerals for everything. There was a period in Europe during which using zero, or the "cipher", as they called it then, could get you imprisoned or even executed.)
Chinese mathematicians beat the Europeans by two millennia in using negative numbers. (Humorous note: When the Indians were writing, they used the "plus" sign, "+", to indicate negative numbers.)
Affiliate
Were Europeans the only ones who didn't "get" negative numbers?
Europeans were not alone in being ignorant of, or dismissive of, or even morally opposed to, negative numbers. Egyptians, nearly two thousand years ago, regarded negative numbers as being ridiculous. Europeans, like the Egyptians, used a system of mathematics that was based purely on geometrical concepts such as area, which is always positive.
This retarded their mathematical progress, because they were thinking of numbers in an unhelpful way. However, when European scholars started translating Arabic texts obtained from North Africa, they were finally exposed to new ways of thinking, and Europe started catching up to the Indians, Chinese, and North-African Arabs.
The point of this history lesson is to explain that many generations of very intelligent people were unable to accept, let alone understand, negative numbers. (Source [PDF]) So if you're having difficulty with the concept, you're in good company. But you, like those eighteenth-century Europeans, can finally "get it", too!
What are negative numbers?
Negative numbers are the numbers that are less than zero. On the number line, the negative numbers are the ones to the left of zero.
How do you recognize negative numbers?
Negative numbers are designated by the "minus" sign in front of them; for instance, "negative five" is written as −5. If you're plotting points on the number line, negative numbers are the ones to the left of zero.
When you first learned your numbers, way back in elementary school, you started with the counting numbers: 1, 2, 3, 4, 5, 6, and so on. Your number line looked something like this:
Later on, you learned about zero, fractions, decimals, square roots, and other types of numbers, so your number line started looking something like this:
Addition, multiplication, and division always made sense — as long as you didn't try to divide by zero — but sometimes subtraction didn't work. If you had "9 − 5", you got 4:
...but what if you had "5 −"9"? You just couldn't do this subtraction, because there wasn't enough "space" on the number line to go back nine units:
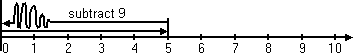
Content Continues Below
You can solve this "space" problem by using negative numbers. The "whole" numbers start at zero and count off to the right; these are the positive integers. The negative integers start at zero and count off to the left:
Note the arrowhead on the far right end of the number line above. That arrow tells you the direction in which the numbers are getting bigger. In particular, that arrow also tells you that the negatives are getting smaller as they move off to the left. For example, −5 is smaller than −4.
How does the expanded number line help us do subtraction?
For starters, by using the number line that has been expanded to the left into negative numbers, we can now do the subtraction "5 − 9". From zero, we go five units to the right, and then we subtract nine units to the left, as shown below:
We end up four units to the left of zero, so we now know that 5 − 9 = −4.
Negative numbers might seem a bit weird at first, but that's okay; negatives take some getting used to. Let's look at a few inequalities, to practice your understanding. Refer to the number line below, as necessary.
- Complete the following inequality: 3 _____ 6
Look at the number line above. Since 6 is to the right of 3, then 6 is larger, so the correct inequality is:
3 < 6
- Complete the following inequality: −3 _____ 6
Look at (or think of) the number line again. Every positive number is to the right of every negative number, so the correct inequality is:
−3 < 6
- Complete the following inequality: −3 _____ −6
Think of the number line again. Since −6 is to the left of −3, then −3, being further to the right, is actually the larger number. So the correct inequality is:
−3 > −6
-
Complete the following inequality: 0 _____ 1
Zero is less than any positive number, so:
0 < 1
- Complete the following inequality: 0 _____ −1
Zero is greater than any negative number, so:
0 > −1
URL: https://www.purplemath.com/modules/negative.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()