Systems of Linear Inequalities (page 2 of 2)

The solution region for the previous example is called a "closed" or "bounded" solution, because there are lines on all sides. That is, the solution region is a bounded geometric figure (a triangle, in that case). You can also obtain solutions that are "open" or "unbounded"; that is, you will have some exercises which have solutions that go off forever in some direction. Here's an example:

• Solve the following system:

2x – y > –3
4x + y < 5

As usual, I first want to solve these inequalities for "y". I get the rearranged system:

y < 2x + 3
y < –4x + 5

Graphing the first inequality, I get:
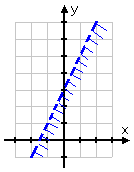
Drawing the second inequality, I get:
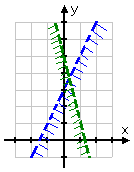
The solution is the lower region, where the two individual solutions overlap.

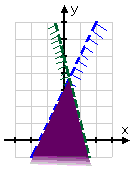
The kind of solution displayed in the above example is called "unbounded", because it continues forever in at least one direction (in this case, forever downward).

Of course, there's always the possibility of getting no solution at all. For instance:

• Solve the following system: Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved

x – y < –2
x – y > 2

First I solve for y, and get the equivalent system:

y > x + 2
y < x – 2

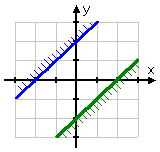
Then I graph the first inequality:
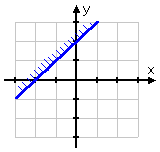
...and then the second:

But there is no place where the individual solutions overlap. (Note that the lines y = x + 2 and y = x – 2 never intersect, being parallel lines with different y-intercepts.) Since there is no intersection, there is no solution.

<< Previous  Top  |  1 | 2  |  Return to Index

  Copyright © 2000-2012  Elizabeth Stapel   |   About   |   Terms of Use

Contact Us