Completing the Square: Circle Equations
Purplemath
The technique of completing the square is used to turn a quadratic expression into the sum of a squared binomial and a number.
In other words, completing the square will convert a generic quadratic into something along the lines of this:
(x − s)2 + t
Content Continues Below
The center-radius form of the circle equation is in this format:
(x − h)2 + (y − k)2 = r2
Affiliate
What is the advantage of the completed-square, center-radius form of a circle's equation?
In completed-square form, the center of the circle is shown as being at the point (h, k) and the radius is shown as being "r". This form of the equation is helpful, because it allows you to easily read off the coordinantes of the center and the length of the radius.
But circle equations are often given in the general format along the lines of:
x2 + y2 + dx + ey + f = 0
When you are given this general form of equation and told to find the center and radius of a circle, you will have to complete the square to convert the equation to center-radius form. This lesson explains how to make that conversion.
What is an example of completing the square to find a circle's center and radius?
- Find the center and radius of the circle having the following equation: 4x2 + 4y2 − 16x − 24y + 51 = 0.
Here is the equation they've given me:
4x2 + 4y2 − 16x − 24y + 51 = 0
First, I'll move the loose number over to the other side of the "equals" sign:
4x2 + 4y2 − 16x − 24y = −51
Now I'll group the x-stuff together, and the y-stuff together:
4x2 − 16x + 4y2 − 24y = −51
Whatever is multiplied on the squared terms (it'll always be the same number), I'll divide it off from every term on each side of the "equals" sign:
Now comes the complicated step. I'll need to insert extra space inside my groupings, because this is where I'll add the squaring term.
To fill in the first parenthetical, I take the x-term coefficient (that is, the number multiplied on the linear x, not the squared x2 term), multiply it by one-half, square the result, and then add this squared value to both sides of the equation. In this case, the number is −4; half of this is −2; the square of this is +4. So I add a +4 inside the x parenthetical, and I also add this to the other side of the equation:
Now I'll do the same with the y-term coefficient: I'll take half of the coefficient, square it, and add the result to each side of the equation. In this case, the coefficient is −6, so half of that is −3, and the square is +9, which I'll add to both sides of the equation:
The values that I got by multiplying by one-half (or, which is the same thing, by dividing in half) are the values for completing the two squares on the left-hand side of my equation:
On the right-hand side of the equation, I need to simplify:
The numerical value on the right-hand side is the square of the length of the radius. In this case, the value is ¼, which is the square of ½:
I've completed the two squares and have found the square of the radius. From this center-radius form of the equation, I can easily read off the solution:
center: (h, k) = (2, 3)
radius:
You can trace the logic in the image below:
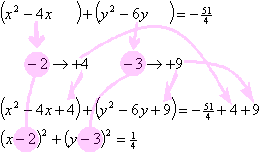
Content Continues Below
What are the steps for completing the square for a circle equation?
- If anything is multiplied on the squared terms (and it'll be the same value on each of the squared-variable terms), then divide through on both sides of the equation by that value.
- Collect the x-containing terms together, and collect the y-containing terms together.
- Move any stand-alone numbers to the other side of the "equals" sign.
- Rewrite the equation, from the previous line, with parentheses around the grouped x and y terms, leaving extra space for a third value to be added in.
- Find half of the coefficients of each of the linear x and y terms (not the squared terms!).
- Square each of these new values.
- Take these squares and ddd (on the left-hand side) inside the appropriate set of parentheses; add (on the right-hand side) to any existing numerical value(s).
- Convert the parentheticals on the left-hand side to completed-square form by replacing the quadratic with the variable and the value you found for that variable in Step 5 above. Remember to put a superscripted 2 on each set of parentheses.
- Convert the numerical expression on the right-hand side to radius form by simplifying
- Find the value of the radius by taking the square root of this simplified value.
Completing the square to find a circle's center and radius always works in this manner. Always do the steps in this order, and each of your exercises should work out fine. (Also, if you get in the habit of always working the exercises in the same manner, you are more likely to remember the procedure on tests.)
Warning: Don't misinterpret the final equation. Remember that the circle formula is:
(x − h)2 + (y − k)2 = r2
If you end up with an equation like this:
(x + 4)2 + (y + 5)2 = 5
...you have to keep straight that h and k are subtracted in the center-radius form, so you really have this equation:
(x − (−4))2 + (y − (−5))2 = 5
Affiliate
That is, the center, based on the equation above, is at the point (−4, −5), not at (4, 5). Be careful with those signs; don't just "read off the answer" without thinking.
Also, remember that the formula says "r2", not "r", so the radius in this case is , not 5.
In the course of the above procedure, about the only other thing that can be a problem is forgetting the sign on the step where you multiply by one-half. Advisory: If you drop a "minus" sign, you'll get the wrong answer for the coordinates of the center, so be careful of this. Don't try to do this step in your head: write it out!
- Find the center and radius of the circle with the following equation: 100x2 + 100y2 − 100x + 240y − 56 = 0.
This is the equation they've given me:
100x2 + 100y2 − 100x + 240y − 56 = 0
First, I'll divide through by the coefficient of the squared terms (that is, I'll divide through by 100):
x2 + y2 − x + 2.4y − 0.56 = 0
Second, I'll group with x terms and the y terms together:
x2 − x + y2 + 2.4y − 0.56 = 0
Third, I'll move the loose numerical term over to the other side of the "equals" sign:
x2 − x + y2 + 2.4y = 0.56
Fourth, I'll rewrite the equation with parentheses around my grouped terms on the left-hand side, leaving space for the squared values that I'll shortly be adding:
(x2 − x ) + (y2 + 2.4y ) = 0.56
Advertisement
Fifth, I'll find half of the coefficients of the linear variable terms. In this case, the coefficient of x is −1 (of which half is −½) and the coefficient of y is +2.4, or +12/5 (of which half is +6/5).
Sixth, I'll square each of these values. For the x parentheses, I'll be using the square of −½, which is +¼; for the y parentheses, I'll be using the square of +6/5, which is +36/25.
Seventh, I'll add these squared terms inside their respective parentheticals on the left-hand side of the equation, and also to the numerical value on the right-hand side of the equation. (For simplicity's sake, I'll also convert the decimal form of the numerical value into fractional form. This will be helpful shortly, when I simplify on that side.)
Eighth, I'll rewrite the parentheticals on the left-hand side of the equation in completed-square form:
Ninth, I'll simplify the numerical stuff on the right-hand side of the equation:
Tenth, I'll finish up by finding the value of the radius, which is the square root of the value on the right-hand side of the equation:
Now I have the equation in center-vertex form, so I can read the coordinates of the center from the equation; the radius is the square root that I just found. So my answer is:
center:
radius:
The animation below shows the tricky part, in the middle, of finding the values for completing the squares and for adding to the right-hand side:
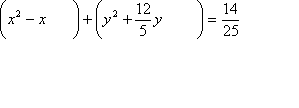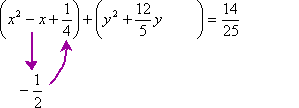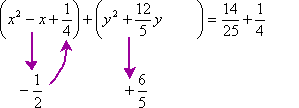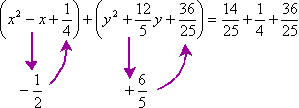
My best advice for you is to do extra completing-the-square exercises. The steps in the process start to become somewhat automatic once you've done twenty, thirty, fifty of them. Keep practicing until you can consistently and quickly work through the steps to get your answers.
URL: https://www.purplemath.com/modules/sqrcircle.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()