Solving & Factoring Polynomials: Examples
Purplemath
These exercises can be very long, so I've only shown three examples so far. Here are a few more, for practice:
-
Find the real-number solutions to x6 + 9x5 + 11x4 − 22x3 − 9x2 − 11x + 21 = 0.
They've given me an equation, and have asked for the solutions to that equation. So I'll be finding x-values, rather than factors.
First, I'll try the trick with 1 and −1. Trying x = 1, I get:
1 + 9 + 11 − 22 − 9 − 11 + 21 = 0
Content Continues Below
Excellent! So x = 1 is one of the zeroes. Trying x = −1, I get:
1 − 9 + 11 + 22 − 9 + 11 + 21 = 48
Okay; so that one isn't a zero. But, to reduce my polynomial by the one factor corresponding to this zero, I'll do my first synthetic division:
![x = 1 is outside on the left; the first row inside is 1 9 11 −22 −9 −11 21; the second row is [empty space] 1 10 21 −1 −10 −21; the answer row is 1 10 21 −1 −10 −21 0](polysolv/solve13.gif)
So my reduced polynomial is equation is:
x5 + 10x4 + 21x3 − x2 − 10x − 21 = 0
This is so nasty... I'm gonna try the trick with x = 1 again, just in case it's a root twice:
1 + 10 + 21 − 1 − 10 − 21 = 0
Nice! Okay; here's my second synthetic division:
![synthetic division with x = 1 outside at the left; the first row inside is 1 10 21 −1 −10 −21; the second row is [empty space] 1 11 32 31 21; the answer row is 1 11 32 31 21 0](polysolv/solve14.gif)
Alright. My new polynomial equation now is:
x4 + 11x3 + 32x2 + 31x + 21 = 0
All the coefficients are positive, so +1 cannot be a zero again. Now it's time for the Rational Roots Test:
x = ±1, 3, 7, 21
Hm... I've already scratched off ±1 directly. Because all the coefficients are positive, then I know that +3, +7, and +21 are out, too. I'd rather stay small, if I can, so I'll try −3 next:
![synthetic division with x = −3 outside at the left; the first row inside is 1 11 32 31 21; the second row is [empty space] −3 −24 −24 −21; the answer row is 1 8 8 7 0](polysolv/solve15.gif)
So now my polynonial equation is:
x3 + 8x2 + 8x + 7 = 0
From this reduced polynomial, I can see that I can cross −21 and −3 off the list of possible roots; they clearly won't work in this reduced polynomial. So I guess I'm left with −7:
![synthetic division with x = −7 outside at left; the first row inside is 1 8 8 7; the second row is [empty space] −7 −7 −7; the answer row is 1 1 1 0](polysolv/solve16.gif)
And now I'm down to a quadratic, which I can easily solve:
x2 + x + 1 = 0
Because there's a minus inside the radical, I know that the solutions of this quadratic are complex numbers; it has no real zeroes. Since they asked for just the real-valued roots of the original polynomial, then I can ignore these last two zeroes. Then my answer is:
x = 1, −3, −7
I didn't check the graph when I did the above, but it does confirm my answer:
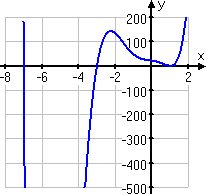
The intercepts at x = −7 and at x = −3 are clear. The intercept at x = 1 is clearly repeated, because of how the curve bounces off the x-axis at this point, and goes back the way it came.
Note: This polynomial's graph is so steep in places that it sometimes disappeared in my graphing software. I had to fiddle with the axis values and window size to get the whole curve to show up. When using your calculator, don't stick only with the default screen for graphs; play with the axis values until you get a picture that's useful.
Content Continues Below
-
Factor completely: 2x5 − 3x4 − 9x3 + 3x2 − 11x + 6
They've given me an expression rather than an equation, and have told me to factor. So I'll be finding factors rather than x-values, and I'll need to keep track of everything I pull out, from beginning to end.
There is no factor common to all terms, so there is nothing to pull out yet. I'll check for zeroes of the associated polynomial equation (setting the original expression equal to zero), and see what I can find. Then I'll convert the zeroes to factors, and pull them out.
First, I'll try the usual shortcut with ±1; the positive first:
2 − 3 − 9 + 3 − 11 + 6 = −12
No joy. I'll try the negative now:
−2 − 3 + 9 + 3 + 11 + 6 = 90
That's even worse. Okay, now I'll use the Rational Roots Test to create a list of maybe-solution values:
I already know that I can ignore ±1. Descartes' Rule of Signs tells me that there will be four, two, or zero positive roots; and one (definite) negative root. So I'll start with the negative integers:
![synthetic division with −2 outside on the left; the first row inside is 2 −3 −9 3 −11 6; the second row inside is [empty space] −4 −14 −10 14 −6; the answer row is 2 −7 5 −7 3 0](polysolv/solve19.gif)
Okay; I've found that x = −2 is a root, which means that x + 2 is a factor. Also, I've reduced the expression still needing to be factored to:
2x4 − 7x3 + 5x2 − 7x + 3
The constant term is 3, so I know that ±2 cannot be a solution to what's left, nor can ±6. Also, I've already found the one negative zero. So this leaves me with:
I'm trying to avoid fractions, so I'll try the last integer possibility:
![synthetic division with 3 outside on the left; the first row inside is 2 −7 5 −7 3; the second row inside is [empty space] 6 −3 −6 −3; the answer row is 2 −1 2 −1 0](polysolv/solve20.gif)
The last row above is a four-term polynomial that looks like it can be factored in pairs:
(2x3 − x2) + (2x − 1)
x2 (2x − 1) + 1(2x − 1)
(2x − 1)(x2 + 1)
The quadratic factor is the sum of squares, so it isn't factorable. This means I'm done, and my complete factorization is:
(x + 2)(x − 3)(2x − 1)(x2 + 1)
Affiliate
Affiliate
The method for answering the two exercises above is the method that I learned, back in the olden times when dinosaurs ruled the world and calculators were made with bear skins and stone knives. It's probably at least similar to the method that you've seen in your book, and your instructor likely expects you do show work along the lines of what I did above.
However, if you have a graphing calculator (and nearly everybody does, nowadays), you can avoid wasting quite so much time on maybe-solution values that turn out not to work.
-
Find all zeroes of y = 8x5 − 58x4 + 137x3 − 118x2 + 33x + 18
Before doing anything else, I'll do a quick graph:
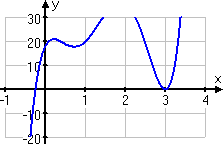
Looking at the graph, I know to check x = 3 twice:
![synthetic division by x = 3, twice; first row is 8 −25 137 −118 33 18; second row is [empty space] 24 −102 105 −39 −18; first answer row is 8 −34 35 −13 −6 0, this row being the first row of the second division; second row is [empty space] 24 −30 15 6; second answer row is 8 −10 5 2 0](polysolv/solve22.gif)
The original polynomial was degree-five. I've found one zero of multiplicity two, which leaves at most three more zeroes. Looking at the polynomial represented by the last row above, the Rational Roots Test says that any remaining "nice" zeroes will be among these:
Clearly, there are no other positive zeroes. On the negative side, the graph suggests that the only value left that I should probably check is :
![synthetic division with −(1/4) outside at left; first row inside is 8 −10 5 2; second row inside is [empty space] −2 3 −2; answer row is 8 −12 8 0](polysolv/solve23.gif)
Now I can see that there's a common factor of four that can be divided out and discarded, leaving me with:
2x2 − 3x + 2 = 0
They asked me for all of the zeroes, not just all of the real-valued ones, so I have to include these two roots that don't show up on the graph. However, by checking the graph first, I was able to save a lot of time in arriving at my answer:
Advertisement
There is a variant of these exercises, where they provide one or more factors (of an expression) or zeroes (of an equation or function), and they want you to find the rest of them. I've got examples of how this works in the last page of the lesson on synthetic division. Varient exercises are often a bit messier and, to answer them, you're expected to have a deeper understanding of how the Quadratic Formula generates solutions in pairs, because of the "±". Otherwise, they work in pretty much the same way.
URL: https://www.purplemath.com/modules/solvpoly3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



