Solving Log Equations with Exponentials
Purplemath
The second type of log equation requires the use of The Relationship:
—The Relationship—
y = bx
...........is equivalent to............
(means the exact same thing as)
logb(y) = x
In animated form, the two equations are related as shown below:
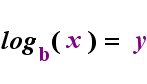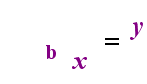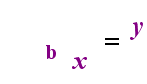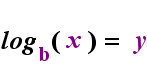
Content Continues Below
Note that the base in both the exponential form of the equation and the logarithmic form of the equation is "b", but that the x and y switch sides when you switch between the two equations. If you can remember this — that whatever had been the argument of the log becomes the "equals" and whatever had been the "equals" becomes the exponent in the exponential, and vice versa — then you should not have too much trouble with solving log equations.
-
Solve log2(x) = 4
Since this equation is in the form "log(of something) equals a number", rather than "log(of something) equals log(of something else)", I can solve the equation by using The Relationship:
log2(x) = 4
24 = x
16 = x
Advertisement
-
Solve log2(8) = x.
I can solve this by converting the logarithmic statement into its equivalent exponential form, using The Relationship:
log2(8) = x
2x = 8
But 8 = 23, so I can equate powers of two:
2x = 23
x = 3
Note that this could also have been solved by working directly from the definition of a logarithm.
What power, when put on "2", would give you an 8? The power 3, of course!
If you wanted to give yourself a lot of work, you could also do this one in your calculator, using the change-of-base formula:
log2(8) = ln(8) / ln(2)
Plug this into your calculator, and you'll get "3" as your answer. While this change-of-base technique is not particularly useful in this case, you can see that it does work. (Try it on your calculator, if you haven't already, so you're sure you know which keys to punch, and in which order.) You will need this technique in later problems.
Affiliate
I'm not saying that you'll necessarily want to solve equations using the change-of-base formula, or always by using the definition of logs, or any other particular method. But I am suggesting that you should make sure that you're comfortable with the various methods, and that you shouldn't panic if you and a friend used totally different methods for solving the same equation.
Affiliate
-
Solve log2(x) + log2(x − 2) = 3
I can't do anything with this equation yet, because I don't yet have it in the "log(of something) equals a number" form. So I'll need to use log rules to combine the two terms on the left-hand side of the equation:
log2(x) + log2(x − 2) = 3
log2[(x)(x − 2)] = 3
log2(x2 − 2x) = 3
Now the equation is arranged in a useful way. At this point, I can use The Relationship to convert the log form of the equation to the corresponding exponential form, and then I can solve the result:
log2(x2 − 2x) = 3
23 = x2 − 2x
8 = x2 − 2x
0 = x2 − 2x − 8
0 = (x − 4)(x + 2)
x = 4, −2
But if x = −2, then "log2(x)", from the original logarithmic equation, will have a negative number for its argument (as will the term "log2(x − 2)"). Since logs cannot have zero or negative arguments, then the solution to the original equation cannot be x = −2.
Then my solution is:
x = 4
Keep in mind that you can always check your answers to any "solving" exercise by plugging those answers back into the original equation and checking that the solution "works". In this case, I'll plug my solution value into either side of the original equation, and verify that each side evaluates to the same number:
the left-hand side:
log2(x) + log2(x − 2)
= log2(4) + log2(4 − 2)3
= log2(4) + log2(2)
= log2(22) + log2(21)
= 2 + 1 = 3
The right-hand side of the original equation was already simplified to "3", so this solution checks.
Content Continues Below
-
Solve log2(log2(x)) = 1
This equation may look overly-complicated, but it's just another log equation. To solve this, I'll need to apply The Relationship twice. I start with the original equation and work with the "outer" log:
log2(log2(x)) = 1
The Relationship converts the above to:
21 = log2(x)
2 = log2(x)
Now I'll apply The Relationship a second time:
x = 22
x = 4
Then the solution is:
x = 4
-
Solve log2(x2) = (log2(x))2
First, I'll expand the square on the right-hand side to be the explicit product of two logs:
log2(x2) = [log2(x)]2
log2(x2) = [log2(x)] [log2(x)]
Then I'll apply the log rule to move the "squared" from inside the log on the left-hand side of the equation, taking it out in front of that log as a multiplier:
2·log2(x) = [log2(x)] [log2(x)]
Then I'll move that term from the left-hand side of the equation to the right-hand side:
0 = [log2(x)] [log2(x)] − 2·log2(x)
This equation may look bad, but take a close look. It's nothing more than a factoring exercise at this point. So I'll factor, and then I'll solve the factors by using The Relationship:
0 = [log2(x)] [log2(x) − 2]
log2(x) = 0 or log2(x) − 2 = 0
20 = x or log2(x) = 2
1 = x or 22 = x
1 = x or 4 = x
Then my solution is:
x = 1, 4
You can use the Mathway widget below to practice solving logarithmic equations (or skip the widget and continue with the lesson). Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/solvelog2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()