Using Slope and y-Intercept to Graph Lines
Purplemath
You've probably already seen the basic method for graphing straight lines; namely, make a T-chart, plot some points, put your ruler against them, and draw the line. But the "nice" form of a straight line's equation (being the slope-intercept form, y = mx + b) can make graphing even simpler and faster.
Given two points (x1, y1) and (x2, y2), the formula for the slope of the straight line going through these two points is:
Content Continues Below
...where the subscripts merely indicate that we have a "first" point (whose coordinates are subscripted with a "1") and a "second" point (whose coordinates are subscripted with a "2"); that is, the subscripts indicate nothing more than the fact that we have two points that we're working with. Note that which point we pick as the "first" point is irrelevant; if we pick the other point to be "first", the subtractions will be reversed, but we'll still get the exact same value for the slope:
(If you're not sure that the two formulas above give exactly the same values, no matter what pair of points is plugged into them, then pick some points and try them out. See what you get.)
Affiliate
The formula for slope is sometimes referred to as "rise over run", because the fraction onsists of the "rise" (being the change in y, going up or down) divided by the "run" (being the change in x, going from left to the right). If you've ever done roofing, built a staircase, graded landscaping, or installed gutters or outflow piping, you've probably encountered this "rise over run" concept. The point is that slope tells us how much y is changing for every so much that x is changing. For example, the slope might (in "real life") tell you that, for every one meter that you move toward the street, your yard slopes downward by five centimeters.
Pictures can be helpful, so let's start our exploration by looking at the following line:
For this equation, we'll look at the line, compute the slope, and consider the y-intercept.
To find some points from the line equation, we have to pick values for one of the variables, and then we must compute the corresponding values of the other variable. Since there is a fraction multiplied on the x, and that fraction has a denominator of 3, I'm going to pick values which are multiples of 3, so the denominator cancels off. Whole numbers are easier, right?
So let's start by picking x = −3. Plugging this in, we get:
So the point we found on the line is (−3, −6) If we then pick x = 0, we get:
The point we found this time is (0, −4). And now that we have two points on the line, we can find the slope of that line from the slope formula:
Let's look at these two points on the graph:
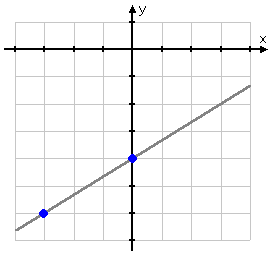
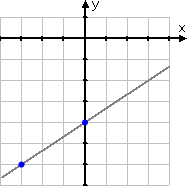
In stair-stepping to the right, going from the first point to the second point, our "path" can be viewed as forming a right triangle:
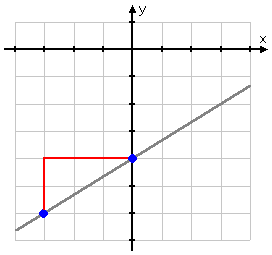
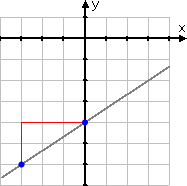
The vertical distance between the y-values of the two points (that is, the height of the triangle) is the "y2 − y1" part of the slope formula. The horizontal distance between the x-values (that is, the side-to-side width of the triangle) is the "x2 − x1" part of the slope formula. The line we need to graph is the hypotenuse of the right triangle.
Note that the slope for this equation and graph is , or "two over three". To go from the first point to the second, we go "up two and over three". This relationship between the slope of a line and pairs of points on that line is always true; for a line equation"y = mx + b", the "up and over" values can always be obtained from the value of m.
Content Continues Below
Having found two points on the line, we can continue to use this "up two, over three" to find further points for the line (and we'll want to plot at least three points, to make sure everything is lining up correctly).
To get to the "next" point on this line, we don't have to do any computationes. Instead, we can go up another two (to y = −2), and over another three to the right (to x = 3), giving us:
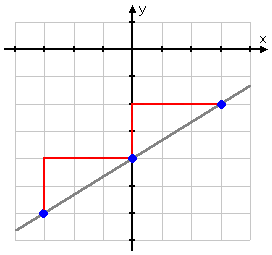
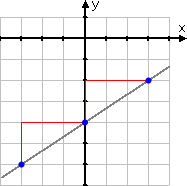
With these three points, we have confirmed the graph of .

(If you're not sure of validity of that last point, then put 3 in for x in the line equation, and verify that you do indeed get −2 for y.)
By the way, did you notice that the line's equation had a "minus four", and the line crossed the y-axis at −4? This always happens; the y-intercept (that is, the place where the line crosses the y-axis) for a straight line with equation "y = mx + b" is always going to be at y = b.
Affiliate
In the previous example, we started with a graphed line and its equation, found a couple points on the line, found the slope and the y-intercept, and noticed the connection between the line's equation, the values of m and b, and how the equation graphed. Let's try another line equation, but this time we won't start with the graph. Instead, we'll use the equation to find the graph quickly and easily, with a minimum of plotting needed.
Advertisement
Our new equation is:
We've learned that the number multiplied onto the x is the slope, so the slope is m = −2 for this line. "But wait!", I hear you cry; "There is only an 'up' (well, a 'down') for this slope; there isn't any 'over'!" Yes, you're right... sort of. But we can deal with this by remembering that any number can be put over "1".
In this case, we can use that fact to convert the slope value into a fraction. By putting the −2 over a 1, we get a slope value of . By using this trick, the slope is now reformatted so as to tell us clearly that, from whatever is our first point, we can get to the "next" point by going "down two, and over one".
Let's start easy with our input values, and use x = 0. Plugging this in, we get:
y = −2(0) + 3 = 0 + 3 = 3
So the point (0, 3) is on the line, and is the point where the line crosses the y-axis. In fact, we didn't even need to plug zero in for the variable, because we can see, right in the line's equation, that the y-intercept is going to be at b = 3. So let's plot that point:
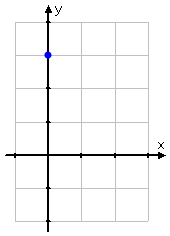
Now that we've got our first point, we can use the slope value to find more points. Our restated slope value of tells us that, in going from one point to the (most convenient) next point, we will be going "down two and over one". (The "down" comes from the "minus" sign on the slope's value. The "over" is always a move to the right, but the sign on the slope can have us moving either up or down.) So, going down two and over one from the intercept to get to the next point, we land at the point (1, 1):
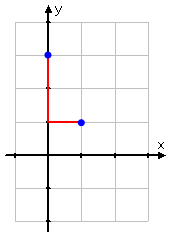
Going down another two, and over another one, we get to the next (convenient) point, (2, −1):
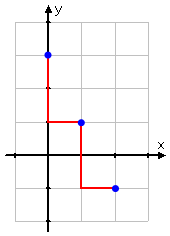
Then the point (2, −1) is also on this line. And with these three points, we can graph the line:
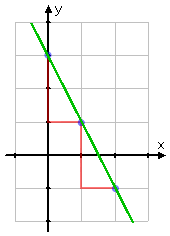
When you have the equation of a straight line, you can always do quick and easy graphing by starting with the y-intercept value, and then plotting other points by using the slope value. In "real life", this may not work so well. For instance, I probably wouldn't try eye-balling the plot points for an equation like, say, y = 0.0062x − 379.04. Instead, I'd use software to get decimal approximations for the plot points. But, for most algebra-class exercises, the above method will work just fine, and can be a real time-saver on tests.
URL: https://www.purplemath.com/modules/slopgrph.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()