|
|
|
|
|
|
|
||
|
|
|
|
|
Simplifying with Nested Parentheses (page 2 of 3) When you have parentheses inside of parentheses, this is called "nested" parentheses. The process works the same way, but you do need to be a little more careful.
When you have nested parentheses like this, the safest plan is to work from the inside out. So I'll take the 3 through the inner parentheses first, before I even think about dealing with the 4 and the brackets. I'll also simplify as I go along. Note that I write each step out completely as I go: 4[x + 3(2x + 1)]
By the way, there is no particular significance to brackets ("[" and "]") versus parentheses versus curly braces ("{" and "}"). Using the different grouping symbols is just a nice way of helping the user keep track of the different pairs of symbols. This is similar to working in an Excel spreadsheet, where the pairs of parentheses in a formula are color-coded, as you can see below:
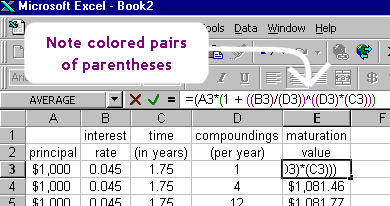
This color-coding helps you see which ")" goes with which "(" in a formula. Using the different types of grouping symbols serves the same purpose in mathematics as the colored parentheses do in the spreadsheet. FYI: The traditional sequence of grouping symbols, working from the inside out, is "parentheses", then "brackets", and then "braces"; then you repeat the sequence, as necessary. But this is not a rule; it's just a tradition.
I won't do anything with the "9 –" or the "+ 4" until I simplify inside the brackets and parentheses. I'll work from the inside out: 9 – 3[x – (3x + 2)]
+ 4 It is not required that you write out this many (or this few) steps. You should be careful to do one step at a time, though, writing things out completely and simplifying as you go. You should do as many steps as you need in order to consistently arrive at the correct answer.
I'll work carefully from the inside out: 5 + 2{ [3 + (2x – 1) + x]
– 2} << Previous Top | 1 | 2 | 3 | Return to Index Next >>
|
|
|
|
Copyright © 2006-2008 Elizabeth Stapel | About | Terms of Use |
|
|
|
|
|
|
