Proof of the Arithmetic Summation Formula
Purplemath
The sum, Sn, of the first n terms of an arithmetic series is given by:
On an intuitive level, the formula for the sum of a finite arithmetic series says that the sum of the entire series is the average of the first and last values, times the number of values being added.
Content Continues Below
This makes sense, especially if you think of a summation visually as being the sum of the areas of the bars pictured below:
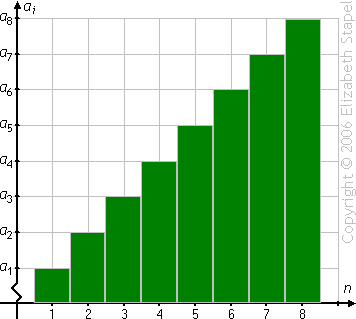
Since the bars grow by a fixed amount at each step, you can, in effect, "average" the bars to get the total area:
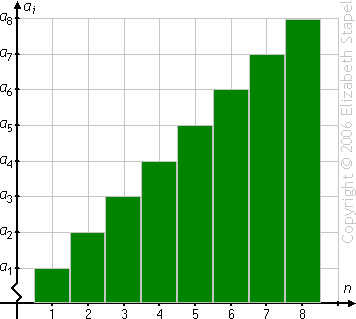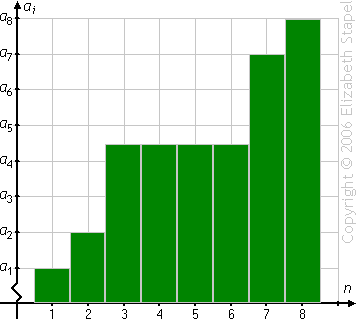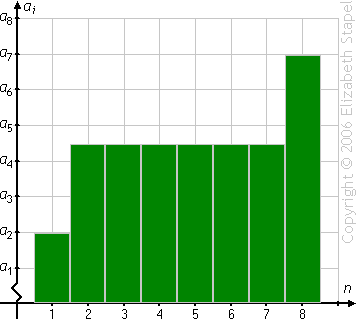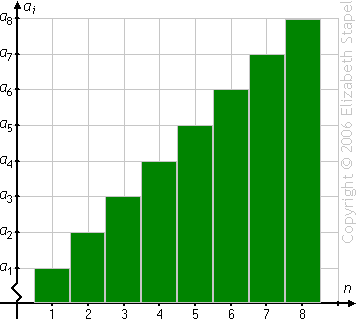
(The above graphic is animated on the "live" page.)
Content Continues Below
While the pictures are helpful in providing a sense of what is going on, they don't prove anything in the mathematical sense. To prove this formula properly requires a bit more work. We will proceed by induction:
Prove that the formula for the n-th partial sum of an arithmetic series is valid for all values of n ≥ 2.
Proof: Let n = 2. Then we have:
For n = k, assume the following:
Let n = k + 1. Then we have:
By nature of arithmetic sequences, we have:
ak = ak+1 – d
ak+1 = a1 + kd
Then, substituting the above into the n = k + 1 expression, we have:
Therefore the result holds for n = k + 1, and the formula is proved for all n ≥ 2. Q.E.D.
URL: https://www.purplemath.com/modules/series6.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



